假设要抽查某企业生产的某种品牌的袋装牛奶的质量是否达标.现从850袋牛奶中抽取50袋进行检验.利用随机数表抽取样本时.先将850袋牛奶按001,002.-.850进行编号.如果从随机数表第3行第1组数 ——青夏教育精英家教网—

13.假设要抽查某企业生产的某种品牌的袋装牛奶的质量是否达标.现从850袋牛奶中抽取50袋进行检验.利用随机数表抽取样本时，先将850袋牛奶按001,002，…，850进行编号.如果从随机数表第3行第1组数开始向右读，最先读到的4袋牛奶的编号是614,593,379,242，请你以此方式继续向右读数，随后读出的4袋牛奶的编号是　　　　，　　　　，　　　　，　　　　.(下面摘取了随机数表第1行至第5行)

78 226　85 384　40 527　48 987　60 602　16 085　29 971　61 279

43 021　92 980　27 768　26 916　27 783　84 572　78 483　39 820

61 459　39 073　79 242　20 372　21 048　87 088　34 600　74 636

63 171　58 247　12 907　50 303　28 814　40 422　97 895　61 421

42 372　53 183　51 546　90 385　12 120　64 042　51 320　22 983

答案

一、选择题(本大题共10小题，每小题4分，共40分)

1.B　2.C　3.D　4.C　5.A　6.C　7.B　8.A　9.C　10.A

二、填空题(本大题共4小题，每小题4分，共16分)

11.－4,13

12.75,83

13.203　722　104　088

14.0.2

三、解答题(本大题共3小题，共34分.)

15.(本题满分10分)

解：程序框图如下：

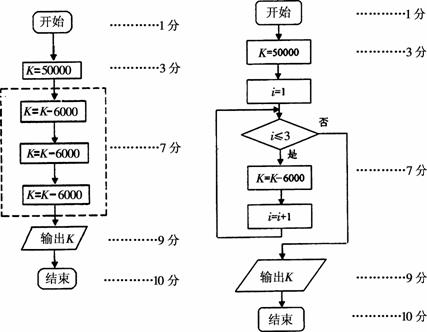
由其他算法得到的程序框图如果合理，请参照上面评分标准给分.

16.(本题满分12分)

解：_甲＝(60＋80＋70＋90＋70)＝74………………………………………………………………2分

_乙＝(80＋60＋70＋80＋75)＝73………………………………………………………………4分

s_甲＝＝＝2………………………………………………………………6分

s_乙＝＝＝2………………………………………………………………8分

∵_甲>_乙，_甲>_乙………………………………………………………………10分

∴甲的平均成绩较好，乙的各门功课发展较平衡………………………………………………………………12分

17.(本题满分12分)

解：(1)分别记白球为1,2,3号，黑球为4,5号.从口袋中每次任取一球，每次取出不放回，连续取两次，其一切可能的结果组成的基本事件(第一次摸到1号，第二次摸到2号球用(1,2)表示)空间为：Ω＝{(1,2)，(2,1)，(1,3)，(3,1)，(1,4)，(4,1)，(1,5)，(5,1)，(2,3)，(3,2)，(2,4)，(4,2)，(2,5)，(5,2)，(3,4)，(4,3)，(3,5)，(5,3),（4,5)，(5,4)}，共有20个基本事件，且上述20个基本事件发生的可能性相同. ………………………………………………………………4分

记“取出的两只球都是白球”为事件A. ………………………………………………………………5分

A＝{(1,2)，(2,1)，(1,3)，(3,1)，(2,3)，(3,2)}，共有6个基本事件. ………………………………………7分

故P(A)＝＝.

所以取出的两只球都是白球的概率为.………………………………………………………………8分

(2)设“取出的两只球中至少有一个白球”为事件B，则其对立事件为“取出的两只球均为黑球”. ………9分

＝{(4,5)，(5,4)}，共有2个基本事件. ………………………………………………………………10分

则P(B)＝1－P()＝1－＝………………………………………………………………11分

所以取出的两只球中至少有一个白球的概率为………………………………………………………………12分

卷二

一、填空题(每小题4分，共16分)

1.1；　2.； 3.；4.6 500

二、解答题(本大题共2小题，共14分)

(本题8分)解：(1)从5张卡片中，任取两张卡片，其一切可能的结果组成的基本事件空间为Ω＝{(0,1)，(0,2)，(0,3)，(0,4)，(1,2)，(1,3)，(1,4)，(2,3)，(2,4)，(3,4)}，共有10个基本事件，且这10个基本事件发生的可能性相同. ……1分

记“两张卡片上的数字之和等于4”为事件A.

A＝{(0,4)，(1,3)}，共有2个基本事件. ………………………………………………………………2分

所以P(A)＝＝………………………………………………………………3分

所以，从中任取两张卡片，两张卡片上的数字之和等于4的概率为…………………………………4分

(2)从5张卡片中，有放回地抽取两次卡片，其一切可能的结果组成的基本事件空间为Ω＝{(x，y)|x∈N，y∈N,0≤x≤4,0≤y≤4}，共有25个基本事件. ……………5分

记“两次取出的卡片上的数字之和恰好等于4”为事件B.

B＝{(0,4)，(4,0)，(1,3)，(3,1)，(2,2)}，共有5个基本事件. ……………6分

则P(B)＝＝……………7分

所以，两次取出的卡片上的数字之和恰好等于4的概率为……………8分

6.(本题6分)

解：(Ⅰ)语句“y＝y＋2”的含义是数列{y_n}，满足y_2n_＋₁＝y_2n_－₁＋2，y₁＝2，

y_{2 009}是以2为公差的等差数列的第1 005项，所以y_{2 009}＝2＋1 004×2＝2 010……………2分

(2)语句“x＝x＋3”和“x＝4x”的含义是

x_n_＋₁＝(k∈N^*)，其中x₁＝4；x_2n_＋₁＝4x_2n＝4(x_2n_－₁＋3) ……………4分

即有x_2n_＋₁＋4＝4(x_2n_－₁＋4)令a_n＝x_2n_－₁＋4，则数列{a_n}是以8为首项，4为公比的等比数列，所以a_n＝8×4ⁿ^－¹＝2×4ⁿ，所以x_2n_＋₁＝2×4ⁿ^＋¹－4

令x_2n_＋₁>2^{2 008}－4，即2×4ⁿ^＋¹－4>2^2
008－4，所以2²ⁿ^＋³>2^{2 008}，所以2n＋3>2 008

即2n＋1>2 006，易知输出框中的“n”即为上述的“2n＋1”

因此输出的n值为2 007. ……………6分

其他正确解法按相应步骤给分.