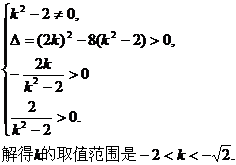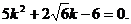1.设全集U=R,集合M={x| x>1},P={x| x2>1},则下列关系中正确的是
A)M=P B) P M C) M
M C) M P
D)
P
D) 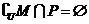
2.已知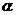 为第三象限角,则
为第三象限角,则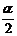 所在的象限是
所在的象限是
A)第一或第二象限 B)第二或第三象限 C)第一或第三象限 D)第二或第四象限
3.在各项都为正数的等比数列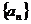 中,首项
中,首项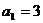 ,前三项和为21,则
,前三项和为21,则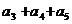 =
=
A)33 B)72 C)84 D)189
4.对于不重合的两个平面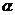 与
与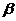 ,给定下列条件:
,给定下列条件:
①存在平面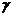 ,使得
,使得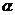 、
、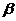 都垂直于
都垂直于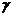 ;
;
②存在平面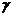 ,使得
,使得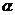 、
、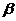 都平行于
都平行于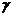 ;
;
③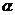 内有不共线的三点到
内有不共线的三点到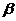 的距离相等;
的距离相等;
④存在异面直线l、m,使得l//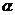 ,l//
,l//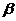 ,m//
,m//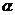 ,m//
,m//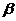 ,
,
其中,可以判定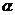 与
与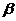 平行的条件有
平行的条件有
A)1个 B)2个 C)3个 D)4个
5.“m=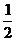 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的
A)充分必要条件 B)充分而不必要条件
C)必要而不充分条件 D)既不充分也不必要条件
6.函数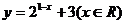 的反函数的解析表达式为
的反函数的解析表达式为
A)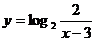 B)
B)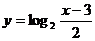 C)
C)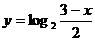 D)
D)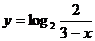
7.若△ABC的内角满足sinA+cosA>0,tanA-sinA<0,则角A的取值范围是
A)(0,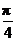 ) B)(
) B)(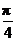 ,
,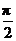 )
C)(
)
C)(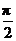 ,
,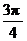 ) D)(
) D)(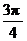 ,p )
,p )
8.设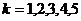 ,则
,则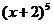 的展开式中
的展开式中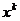 的系数不可能是
的系数不可能是
A)10 B)40 C)50 D)80
9.(理)抛物线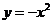 上的点到直线
上的点到直线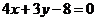 的距离的最小值是
的距离的最小值是
A)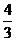 B)
B)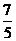 C)
C)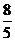 D)3
D)3
(文)抛物线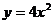 上的一点M到焦点的距离为1,则点M的纵坐标是
上的一点M到焦点的距离为1,则点M的纵坐标是
A)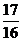 B)
B)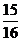 C)
C)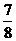 D)0
D)0
10.北京《财富》全球论坛期间,某高校有14名志愿者参加接待工作.若每天排早、中、晚三班,每班4人,每人每天最多值一班,则开幕式当天不同的排班种数为
A)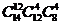 B)
B)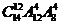 C)
C)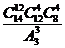 D)
D)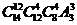
11. 从圆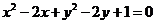 外一点
外一点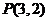 向这个圆作两条切线,则两切线夹角的余弦值为
向这个圆作两条切线,则两切线夹角的余弦值为
A)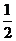 B)
B)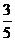 C)
C)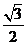 D)
D)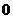
12.长方体ABCD-A1B
A) 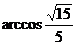 B)
B) 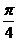 C)
C) 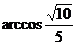 D)
D) 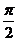
13.若双曲线的渐近线方程为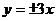 ,它的一个焦点是
,它的一个焦点是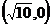 ,则双曲线的方程是
,则双曲线的方程是
14.对于函数f(x)定义域中任意的x1,x2(x1≠x2),有如下结论:
①f(x1+x2)=f(x1)・f(x2);② f(x1・x2)=f(x1)+f(x2); ③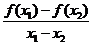 >0;④
>0;④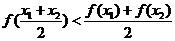 .
.
当f(x)=lgx时,上述结论中正确结论的序号是
15.点A(3,1),B(6,1),C(4,3),D为线段BC的中点,则向量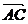 与
与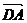 的夹角
的夹角
是
16.(理)若随机变量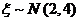 ,则
,则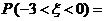 (精确到小数点后4位)(参考值:
(精确到小数点后4位)(参考值:
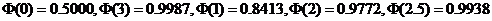 )
)
(文)从某自动包装机包装的食盐中,随机抽取20袋,测得各袋的质量分别为(单位g): 492 496 494 495 498 497 501 502 504 496
497 503 506 508 507 492 496 500 501 499
根据频率分布估计总体分布的原理,该自动包装机包装的袋装食盐质量在497.5~501.5之间的概率约为(用小数表示)
 嵩 明 一 中 高 三 年 级 数 学 测 试 卷 答 题 纸
嵩 明 一 中 高 三 年 级 数 学 测 试 卷 答 题 纸
题号
一
二
三
成绩
17
18
19
20
21
22
分数
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
13._______________________ 14._______________________
15._______________________ 16._______________________
17.(11分)已知函数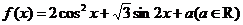 .
.
(1)若x∈R,求f(x)的单调递增区间;(6分)
(2)若x∈[0,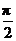 ]时,f(x)的最大值为4,求a的值,并指出这时x的值.(5分)
]时,f(x)的最大值为4,求a的值,并指出这时x的值.(5分)
18.(11分)(理)甲、乙两人在罚球线投球命中的概率分别为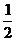 与
与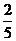 ,投中得1分,投不中得0分
,投中得1分,投不中得0分
(1)甲、乙两人在罚球线各投球一次,求两人得分之和x的数学期望;(5分)
(2)甲、乙两人在罚球线各投球二次,求这四次投球中至少一次命中的概率。(6分)
(文)甲、乙两人在罚球线投球命中的概率分别为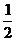 与
与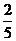
(1)甲、乙两人在罚球线各投球一次,求两人都没投中的概率;(5分)
(2)甲、乙两人在罚球线各投球二次,求这四次投球中至少一次命中的概率。(6分)
19.(13分)直线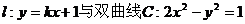 的右支交于不同的两点A、B.
的右支交于不同的两点A、B.
(1)求实数k的取值范围;(6分)
(2)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.(7分)
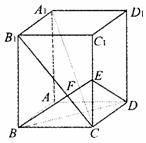 20.(13分)已知长方体ABCD-
20.(13分)已知长方体ABCD-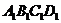 中,棱AB=BC=3,
中,棱AB=BC=3,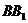 =4,连结
=4,连结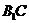 ,过B点作
,过B点作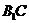 的垂线交
的垂线交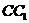 于E,交
于E,交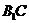 于F.
于F.
(1)求证: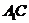 ⊥平面EBD;(3分)
⊥平面EBD;(3分)
(2)求ED与平面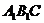 所成角的大小;(5分)
所成角的大小;(5分)
(3)求二面角E-BD-C的大小.(5分)
21.(11分)进货原价为80元的商品400个,按90元一个售出时,可全部卖出。已知这种商品每个涨价一元,其销售数就减少20个,问售价应为多少时所获得利润最大?
22.(11分)设数列{an}的首项a1=a≠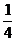 ,且
,且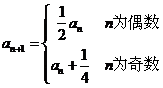 ,
,
记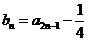 ,n=l,2,3,…・.
,n=l,2,3,…・.
(1)求a2,a3;(4分)
(2)判断数列{bn}是否为等比数列,并证明你的结论;(7分)
嵩 明 一 中 高 三 年 级 数 学 测 试 卷 答 案
(理)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
C
B
B
A
C
C
A
A
B
D
(文)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
A
C
D
B
D
B
C
D
A
C
(理)
13.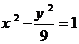 14.②③
14.②③
15.
 16.(理)0.1525 (文)0.25
16.(理)0.1525 (文)0.25
17.解:(1)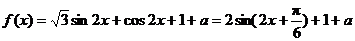 .
.
解不等式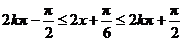 .
.
得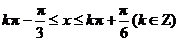
∴ f(x)的单调增区间为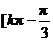 ,
,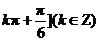 .
.
(2)∵ 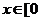 ,
,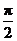 ], ∴
], ∴ 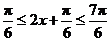 .
.
∴ 当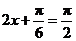 即
即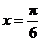 时,
时,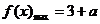 .
.
∵ 3+a=4,∴ a=1,此时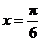 .
.
18.解:(理)(1)依题意,记“甲投一次命中”为事件A,“乙投一次命中”为事件B,则P(A)=,P(B)=,P()=,P()=,甲、乙两人得分之和ξ的可能取值为0、1、2,则ξ的概率分布为
ξ
0
1
2
P
Eξ=0×+1×+2×=
(文)(1)P()=
(2) 甲、乙两人在罚球线各投球二次均不命中的概率为×××=
故甲、乙两人在罚球线各投球二次中至少一次命中的概率为1-=
19.解:(1)将直线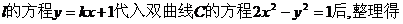
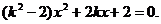 ……①
……①
依题意,直线l与双曲线C的右支交于不同两点,故
(2)设A、B两点的坐标分别为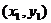 、
、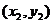 ,则由①式得
,则由①式得
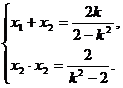 ……②
……②
假设存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F(c,0).
则由FA⊥FB得:
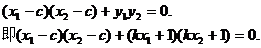
整理得
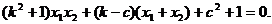 ……③
……③
把②式及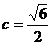 代入③式化简得
代入③式化简得
解得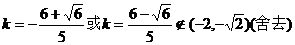
可知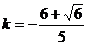 使得以线段AB为直径的圆经过双曲线C的右焦点
使得以线段AB为直径的圆经过双曲线C的右焦点
 20.解: (1)连结AC交BD于O,则AC⊥BD.
20.解: (1)连结AC交BD于O,则AC⊥BD.
又 ∵ 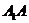 ⊥平面AC, ∴
⊥平面AC, ∴ 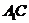 ⊥BD.
⊥BD.
∵ 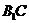 ⊥BE而
⊥BE而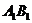 ⊥平面
⊥平面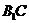 , ∴
, ∴ 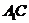 ⊥BE.
⊥BE.
∵ BD 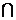 BE=B, ∴
BE=B, ∴ 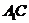 ⊥平面BED.
⊥平面BED.
(2)连结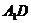 ,由
,由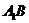 ∥CD知D在平面
∥CD知D在平面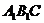 内,由(1)是
内,由(1)是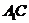 ⊥EB.
⊥EB.
又∵ 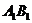 ⊥BE, ∴ BE⊥平面
⊥BE, ∴ BE⊥平面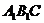 ,即得F为垂足.
,即得F为垂足.
连结DF,则∠EDF为ED与平面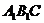 所成的角.
所成的角.
由已知AB=BC=3,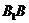 =4,可求是
=4,可求是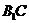 =5,
=5,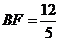 .
.
∴ 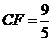 ,
,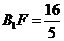 ,则
,则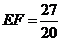 ,
,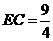 .
.
∴ 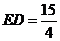 .
.
在Rt△EDF中,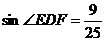 ,
,
∴ ED与平面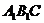 所成的角为
所成的角为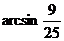 .
.
(3)连结EO,由EC⊥平面BDC且AC⊥BD知EO⊥BD.
∴ ∠EOC为所求二面角E-BD-C的平面角.
∵ 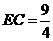 ,
,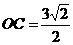 ,
,
∴ 在Rt△EOC中,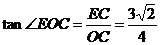 .
.
∴ 二面角E-BD-C的大小为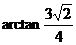 .
.
21.解:设售价为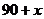 元时利润为
元时利润为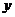 ,此时售量为
,此时售量为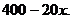
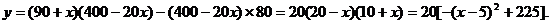 当
当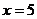 时,
时,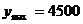 (元)。
(元)。
答:售价为95元时获利最大,其最大值为4500元。
22.解:(I)a2=a1+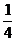 =a+
=a+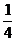 ,a3=
,a3=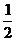 a2=
a2=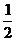 a+
a+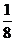 ;
;
(II)bn+1=a2n+1-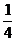 =
=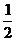 a2n-
a2n-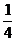 =
=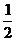 (a2n-1-
(a2n-1-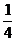 )=
)=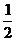 bn, (n∈N*)
bn, (n∈N*)
所以{bn}是首项为a-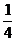 , 公比为
, 公比为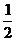 的等比数列・
的等比数列・