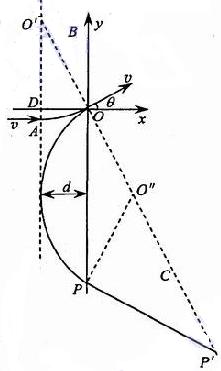
【解析】方法一：（1）设磁场左边界与x轴相交子D点，与CO相交于O’点，由几何关系可知，直线OO’与粒子过O点的速度v垂直。在直角三角形 OO’D中已知∠OO’D =30⁰设磁场左右边界间距为d，则OO’=2d。依题意可知，粒子第一次进人磁场的运动轨迹的圆心即为O’点，圆弧轨迹所对的圈心角为30⁰ ，且OO’为圆弧的半径R。

由此可知，粒子自A点射人磁场的速度与左边界垂直。

A 点到x轴的距离：AD=R(1－cos30⁰)………………………………①

由洛仑兹力公式、牛顿第二定律及圆周运动的规律，得：

                  qvB=mv²/R………………………………………②

联立①②式得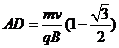：…………………………………③

（2）设粒子在磁场中做圆周运动的周期为T第一次在磁场中飞行的时间为 t₁，有：

t₁=T/12…………………………………………④

T=2πm/qB………………………………………⑤

依题意．匀强电场的方向与x轴正向夹角应为150⁰。由几何关系可知，粒子再次从O点进人磁场的速度方向与磁场右边界夹角为60⁰。设粒子第二次在磁场中飞行的圆弧的圆心为O’’，O’’必定在直线OC 上。设粒子射出磁场时与磁场右边界文于P点，则∠OO’’P =120⁰．设粒子第二次进人磁场在磁场中运动的时问为t₂有：

t₂=T/3…………………………………………⑥

设带电粒子在电场中运动的时间为 t ₃，依题意得：

t₃=T－(t₁+t₂)…………………………………⑦

由匀变速运动的规律和牛顿定律可知：

?v=v?at₃……………………………………⑧

a=qE/m ………………………………………⑨

联立④⑤⑥⑦⑧⑨式可得：

E=12Bv/7π……………………………………⑩

粒子自P点射出后将沿直线运动。

设其由P点再次进人电场，由几何关系知：∠O’’P’P =30⁰……⑾

消

三角形OPP’为等腰三角形。设粒子在P、P’两点间运动的时问为t₄，有：

t₄=PP’/v………………………………………⑿

又由几何关系知：OP=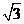R………………………………………⒀

联立②⑿⒀式得：t₄=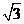m/qB

方法二：（1）从A点进入磁场后从O点离开磁场的过程是匀速圆周运动，画出粒子运动的轨迹图，依题意由几何关系可得圆弧的圆心正好是两条虚线的交点。

故经过A点的速度方向为x轴正方向。

设圆周的半径为R，有：∠OO₁A=30°…………………………………①

根据向心力公式：Bqv = m……………………………………………②

A点到x轴的距离：x= R－Rcos30°…………………………………③

联立①②③解得：x =

（2）粒子能从O点进入电场且能由O点返回，对正电荷，说明电场的方向垂直于OC向左，设电场强度大小为E，电场中的时间为t₁，由动量定理：

Eqt₁=2mv…………………………………………………………………………④

粒子从A点射入到第二次离开磁场所用的时间恰好等于粒子在磁场中做圆周运动的周期T，由：

T= …………………………………………………………………………⑤

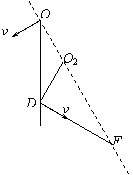从O点返回磁场后的轨迹如图，圆心角为120°，故：

T=t₁＋T＋T………………………………………………………………⑥

联立②④⑤⑥解得：E = ……………………………………………⑦

（3）第二次离开磁场后到再进入电场，如图轨迹。

则DF=OD=2R cos30°………………………………………………………⑧

时间t₂= =