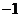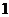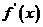(1)已知全集 ,
,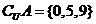 ,
,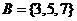 ,则
,则
A. B.
B. C.
C. D.
D.
(2)若a,b是任意实数,且a>b,则
A. B.
B. C.
C.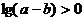 D.
D.
(3)已知 ,则
,则 的取值范围是
的取值范围是
A. B.
B. C.
C. D.
D.
(4)在等差数列{ }中,若
}中,若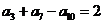 ,
, ,则
,则
A.54 B.
(5)函数 的图象如图所示,则它的解析式是
的图象如图所示,则它的解析式是
A. B.
B.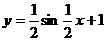
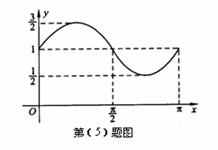 C.
C. D.
D.
(6) 展开式的第四项等于7,则x等于
展开式的第四项等于7,则x等于
A.-5 B.
C. D.5
D.5
(7)经过点 被圆C:
被圆C: 截得的弦最短的直线的方程是
截得的弦最短的直线的方程是
A. B.
B.
C. D.
D.
(8)4名男生与5名女生站成一排,要求4名男生的顺序一定,5名女生的顺序也一定,不同的站法总数为
A.126 B.
(9)若不等式 对一切
对一切 成立,那么
成立,那么 的取值范围是
的取值范围是
A. B.
B. C.
C. D.
D.
(10)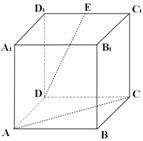 如图,在棱长为2的正方体
如图,在棱长为2的正方体 中,E是
中,E是 的中点,那么异面直线DE和AC所成的角的余弦值等于
的中点,那么异面直线DE和AC所成的角的余弦值等于
A.  B.
B. 
C.  D.
D. 
(11)函数 ,当
,当 时的最小值为
时的最小值为
A. B.
B. C.
C.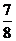 D.1
D.1
(12)已知双曲线中心在原点且一个焦点为 ,直线
,直线 与其相交于M、N两点,MN中点的横坐标为
与其相交于M、N两点,MN中点的横坐标为 ,则此双曲线的方程是
,则此双曲线的方程是
A. B.
B. C.
C.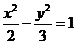 D.
D.
平顶山市2008届高三调研考试
文科数学
第Ⅱ卷
注意事项:
1.答题前,考生先用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚.
2.本卷共10小题,共90分.
一
二
三
总 分
17
18
19
20
21
22
(13)已知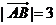 ,
,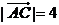 ,
, 与
与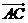 的夹角为60°,则
的夹角为60°,则 与
与 的夹角余弦为 .
的夹角余弦为 .
(14)设 ,式中变量
,式中变量 ,
, 满足
满足 ,则
,则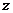 的最小值为_________.
的最小值为_________.
(15)设正四棱锥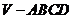 的底面ABCD在一个球的大圆上,顶点V也在这个球面上,那么它的侧面与底面所成的二面角为_______________.
的底面ABCD在一个球的大圆上,顶点V也在这个球面上,那么它的侧面与底面所成的二面角为_______________.
(16)已知定义域为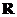 的函数
的函数 是奇函数,那么函数
是奇函数,那么函数 的反函数是___________________________.
的反函数是___________________________.
(17)(本小题满分10分)
 已知
已知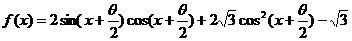 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)设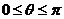 ,且函数
,且函数 为偶函数,求满足
为偶函数,求满足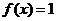 ,
,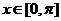 的x的集合.
的x的集合.
(18)(本小题满分12分)
 有一种舞台灯,外形是正六棱柱,在其每一个侧面上安装5只颜色各异的彩灯,假若每只灯正常发光的概率为
有一种舞台灯,外形是正六棱柱,在其每一个侧面上安装5只颜色各异的彩灯,假若每只灯正常发光的概率为 . 若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面进行维修.
. 若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面进行维修.
(Ⅰ)求一个面需要维修的概率;
(Ⅱ)求至少有3个面需要维修的概率.
(19)(本小题满分12分)
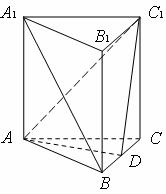 如图,在正三棱柱ABC-A1B1C1中,AB=AA1,D是BC上一点,且AD⊥C1D.
如图,在正三棱柱ABC-A1B1C1中,AB=AA1,D是BC上一点,且AD⊥C1D.
 (Ⅰ)求证:A1B∥平面AC1D;
(Ⅰ)求证:A1B∥平面AC1D;
(Ⅱ)求二面角C-AC1-D的大小.
(20)(本小题满分12分)
设数列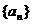 、
、 分别满足
分别满足 ,
, ,
,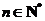 .
.
 (Ⅰ)求数列
(Ⅰ)求数列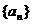 和
和 的通项公式;
的通项公式;
(Ⅱ)若数列 的前
的前 项和为
项和为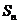 ,试求
,试求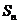 .
.
(21)(本小题满分12分)
已知函数 ,
,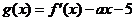 ,其中
,其中 是
是 的导数.
的导数.
 (Ⅰ)对满足
(Ⅰ)对满足 的一切
的一切 的值,都有
的值,都有 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)设直线 是函数
是函数 图象的一条切线,求函数
图象的一条切线,求函数 的单调区间.
的单调区间.
(22)(本小题满分12分)
已知定点 ,过点A作倾斜角为45°的直线l,交抛物线
,过点A作倾斜角为45°的直线l,交抛物线 于B、C两点,且|BC|=
于B、C两点,且|BC|= .
.
 (Ⅰ)求抛物线的方程;
(Ⅰ)求抛物线的方程;
(Ⅱ)在(Ⅰ)中的抛物线上是否存在点D,使得|DB|=|DC|成立?如果存在,求出点D的坐标;如果不存在,请说明理由.
平顶山市2008届高三调研考试
文科数学答案
(17)解:(Ⅰ)
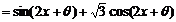 =
=
或 ,
…………3分
,
…………3分
所以, 的最小正周期
的最小正周期 ;
…………5分
;
…………5分
(Ⅱ)当 时,f(x)为偶函数 .
…………7分
时,f(x)为偶函数 .
…………7分
由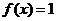 ,得
,得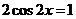 ,所以
,所以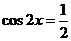 ,
…………8分
,
…………8分
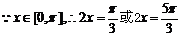 ,
…………9分
,
…………9分
所以,所求x的集合为 . ……………10分
. ……………10分
(18)解:(Ⅰ)因为每面上的5只灯正常发光是5次独立重复试验,所以一个面不需要维修的概率为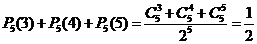 ,
……4分
,
……4分
因此,一个面需要维修的概率为 .
……6分
.
……6分
(Ⅱ)因为六个面是否需要维修是6次独立重复试验,所以,至少有3个面需要维修的概率是 ,
……8分
,
……8分
又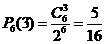 ,
, ,
, ,
, ,
,
因此, 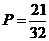 .
……12分
.
……12分
(19)解:(Ⅰ)∵ABC-A1B1C1是正三棱柱,∴ CC1⊥平面ABC,∵ AD⊥C1D,
∴ AD⊥BC, ∴ D是BC的中点.
……3分
连结AC1与A1C相交于E点,在△A1BC中,∵D、E是中点,
∴A1B∥DE,又DE在平面AC1D内,∴A1B∥平面AC1D.
……6分
 (Ⅱ)作CF⊥C1D于F,则CF⊥平面AC1D,连结EF,∵CE⊥AC1
(Ⅱ)作CF⊥C1D于F,则CF⊥平面AC1D,连结EF,∵CE⊥AC1
∴ EF⊥AC1,∴ 则∠CEF就是二面角C-AC1-D的平面角. ……8分∵ ,
,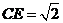 , ……10分
, ……10分
∴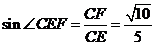 ,
,
即,二面角C-AC1-D的
大小为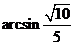 .
……12分
.
……12分
 方法二:设D1是B1C1的中点,以DC为x轴,
方法二:设D1是B1C1的中点,以DC为x轴,
DA为y轴,DD1为z轴建立空间直角坐标系
(如图), ……7分
并设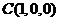 ,则
,则 ,
,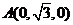 ,
, ,∵AC的中点为
,∵AC的中点为 ,
,
∴ ,
……8分
,
……8分
∴平面AC1C的法向量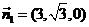 .
……9分
.
……9分
设平面AC1D的法向量为 ,∵
,∵ ,
,
∴ ,∴
,∴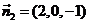 , ……10分
, ……10分
∴ ,
……11分
,
……11分
因此,二面角C-AC1-D的大小为 . ……12分
. ……12分
(20)解:(Ⅰ)∵ ,∴
,∴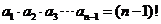 ,
,
∴
当 时,
时, ,而当
,而当 时
时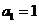 ,∴
,∴ . …………3分
. …………3分
∵ ,∴
,∴  ,
,
∴当 时,
时,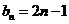 ,而当
,而当 时
时 ,∴
,∴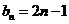 .………6分
.………6分
(Ⅱ)∵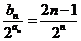 , ∴
, ∴ 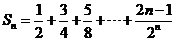 …………8分
…………8分
∴ ,
…………9分
,
…………9分
∴相减得 ,
,
∴ .
…………12分
.
…………12分
(21)解:(Ⅰ)由题意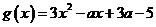 ,
…………2分
,
…………2分
令 ,
, ,
,
对 ,恒有
,恒有 ,即
,即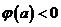 ,
,
∴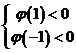 , 即
, 即  ,
…………4分
,
…………4分
解得 .
.
故 时,对满足
时,对满足 的一切
的一切 的值,都有
的值,都有 .………6分
.………6分
(Ⅱ)∵  ,设直线
,设直线 与函数
与函数 相切于点
相切于点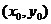 ,
,
则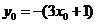 ,
…………7分
,
…………7分
所以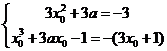 ,即
,即 ,
,
解得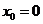 ,
, ,所以
,所以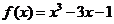 ,
, .…………9分
.…………9分
因此, 是函数
是函数 的单调递增区间;
的单调递增区间;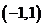 是函数
是函数 的单调递减区间;
的单调递减区间; 是函数
是函数 的单调递增区间. ……………12分
的单调递增区间. ……………12分
(22)解:(Ⅰ)直线l方程为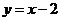 ,将其代入
,将其代入 ,整理为,
,整理为,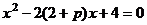 .①
…………2分
.①
…………2分
∵p>0,∴ .
.
设 .
.
∴ .
…………4分
.
…………4分
∵|BC|= ,而
,而 ,
,
∴ ,解得p=1.
,解得p=1.
∴抛物线方程 .
…………6分
.
…………6分
(Ⅱ)假设在抛物线 上存在点
上存在点 ,使得|DB|=|DC|成立,
,使得|DB|=|DC|成立,
记线段BC中点为 .
.
则 .
………8分
.
………8分
当p=1时,①式成为 .
.
∴ ,
, .
.
∴点 应满足
应满足 .
…………10分
.
…………10分
解得, .
.
∴存在点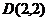 或(8,-4),使得|DB|=|DC|成立.
…………12分
或(8,-4),使得|DB|=|DC|成立.
…………12分