18．解: 原式=　解:原式=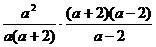-----------4分

            = ------------------------------------------------------------5分

∴原式的值为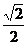---------------------------------------------------6分

19．解：选择（1）和（2）组成方程组（其它组合情况可参照本解法评分）

-----------------------------------------（2分）

（1）+（2）得：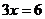

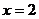---------------------------------------------------（3分）

把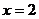代入（1）得：（4分）

∴原方程组的解是  -------------------------------------（6分）

注：（1）和（3）组成的方程组的解是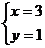，（2）和（3）组成的方程组的解是

20. 解：设竹竿长为x尺。------------------------------------------（1分）

    则：（x?4）²+（x?2）²=x²  ----------------------------------（3分）

x₁=10    x₂=2（不合题意舍去）------------------------（5分）

答：竹竿长为10尺.   ------------------------------------------（6分）

21．解：连结AD

        ∵BC是⊙A的切线

        ∴AD⊥BC ---------------------------------------- (1分)

        ∴S△ABC=1/2BC・AD=1/2×4×2=4 ----------------- (2分)

      又∵∠EPF=40°

        ∴∠BAC=80°

        ∴S扇形ABC=80/360∏×2²=8/9∏ ---------- (4分)

        故：S阴=4-8/9∏ -------------------------(6分)

22. 解：答案不唯一，其它条件参照得分

    添加：N为CD中点---------------------------------------------------------（2分）

证明如下：∵平行四边形ABCD

∴ AB∥CD，又M、N为AB、CD边的中点，

可得四边形AMCN为平行四边形，----------------------（4分）

∴∠AMC=∠ANC

又∵∠B=∠D，

∴∠DAN=∠BCM. ---------------------------------（7分）

23. 解：公路不会穿过森林公园------------------------------------------（1分）

理由：

设AH为x米，

在Rt△AHC中，有

AH＝X　-----------------------------------------（3分）

在Rt△ABH中，有

BH＝X　--------------------------------------------（4分）

∴AH＋BH＝1000

X＝≈366米　---------------------------------（6分）

∴AH＝366米

∵AH＞300

故：公路不会穿过森林公园　------------------------------（7分）

24．解：（1）列表如下：

1

2

3

4

1

（1，1）

（1，2）

（1，3）

（1，4）

2

（2，1）

（2，2）

（2，3）

（2，4）

3

（3，1）

（3，2）

（3，3）

（3，4）

4

（4，1）

（4，2）

（4，3）

（4，4）

由列表可得：P（数字之和为5）=------------------------------------------ （4分）

（2）因为P（甲胜）=，P（乙胜）=------------------------------------ （6分）

∴甲胜一次得12分，要使这个游戏对双方公平，乙胜一次得分应为：

（分）-----------------------------------------------------------（8分）

25. 解：（1）设A型服装单价x元，B型服装单价y元，---------------（1分）

依题意得解得 ----------------------------（4分）

答：（略）-----------------------------------------------------------------------（5分）

     （2）设B型服装购进m件，则A型服装购进（2m+4）件.-----------（6分）

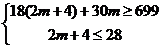依题意得，解得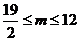 -----------------（9分）

取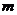=10、11、12，--------------------------------------------------------------（10分）

答：有3种进货方案：

①A--24件，B--10件；②A--26件，B--11件；③A--28件，B--12件.----（11分）

26. 解：（1）由已知条件得：

梯形周长为12，高4，面积为28。

过点F作FG⊥BC于G

过点A作AK⊥BC于K

则可得：FG=×4

∴S△BEF=BE・FG=－x²+x（7≤x≤10）--------------（3分）

（2）存在  -----------------------------------------------------------------（4分）

由（1）得：－x²+x=14得x₁=7       x₂=5（不合舍去）

∴存在线段EF将等腰梯形ABCD的周长与面积同时平分，此时BE=7-----------------（6分）

（3）不存在 ----------------------------------------------------------------------------------（7分）

根据S_△BEF∶S_AFECD=1∶2，(BE+BF)∶(AF+AD+DC)=1∶2 --------------------- （9分）

则有－x²+x=整理得：3x²－24x+70=0    △=576－840<0 ----------------（11分）

∴不存在这样的实数x.

即不存在线段EF将等腰梯形ABCD的周长和面积。

同时分成1∶2的两部分  ----------------------------------------------------------------（12分）