1.已知sin(π+θ)=-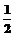 ,则cosθ的值为( )
,则cosθ的值为( )
A.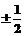 B.
B.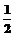 C.
C.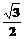 D.
D.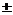
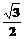
2.定义A-B={x|x∈A且x B},若A={2,4,6,8,10},B={1,4,8},则A-B是( )
B},若A={2,4,6,8,10},B={1,4,8},则A-B是( )
A.{2,6,10} B.{1,2,6,10} C.{1} D.{4,8}
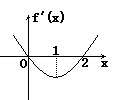
3.已知等比数列{an}的公比为-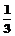 ,则
,则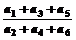 等于( )
等于( )
 A.-
A.-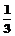 B.
B.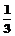 D.3
D.3
4.设f′(x)是函数f(x)的导函数,y=f′(x)的图象如图所示,
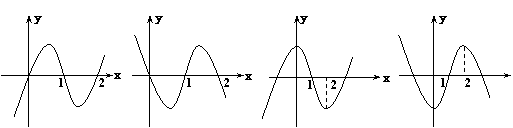 则y=f(x)图象可能为( )
则y=f(x)图象可能为( )
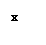
A B C D
5.要得到函数y=sin(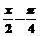 )的图象,只需将函数y=sin
)的图象,只需将函数y=sin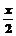 的图象( )
的图象( )
A.向左平移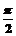 个单位 B.向右平移
个单位 B.向右平移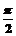 个单位
个单位
C.向左平移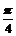 个单位 D.向右平移
个单位 D.向右平移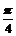 个单位
个单位
6.a=-1是两直线ax+2y+6=0与x+(a-1)y+a2-1=0平行的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.如图所示图形中是四棱锥三视图的是( )
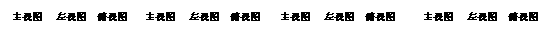
A. B. C. D.
8.已知平面上不同的四点A、B、C、D,若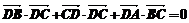 ,则△ABC是( )
,则△ABC是( )
A.等腰三角形 B.等边三角形 C.等腰或直角三角形 D.直角三角形
9.设α、β、γ为平面,m,n,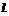 为直线,则m⊥β的一个充分条件是( )
为直线,则m⊥β的一个充分条件是( )
A.α⊥β,α∩β=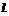 ,m⊥
,m⊥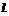 B.α∩γ=m, α⊥γ, β⊥γ
B.α∩γ=m, α⊥γ, β⊥γ
C.α⊥γ, β⊥γ, m⊥α D.n⊥α,n⊥β, m⊥α
10.若2-m与|m|-3异号,则m的取值范围是( )
A.2<m<3 B.-3<m<
11.设椭圆的中心在原点O,右焦点为F,右准线为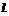 ,如果在
,如果在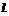 上存在点M,使线段OM的垂直平分线经过F,则椭圆的离心率的取值范围是( )
上存在点M,使线段OM的垂直平分线经过F,则椭圆的离心率的取值范围是( )
A.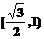 B.
B.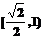 C.
C.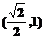 D.
D.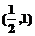
12.函数f(x)=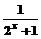 ,则函数在(-∞,+∞)上是( )
,则函数在(-∞,+∞)上是( )
A.单调递减,有最小值 B.单调递减,无最小值
C.单调递增,有最大值 D.单调递增,无最大值
13.已知P(x,y)满足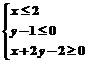 ,则x-y最小值是___________。
,则x-y最小值是___________。
14.已知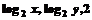 成等差数列,则在平面直角坐标系中,点M(x,y)的轨迹方程是________。
成等差数列,则在平面直角坐标系中,点M(x,y)的轨迹方程是________。
 15.抛物线y=4x2上的一点M到焦点的距离为1,则点M的纵坐标为__________。
15.抛物线y=4x2上的一点M到焦点的距离为1,则点M的纵坐标为__________。
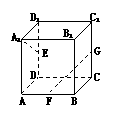
16.长方体ABCD-A1B
是DD1、AB、CC1的中点,则异面直线A1E与GF所成角的大小是________。
17.(12分)在△ABC中,a、b、c分别是角A、B、C的对边,且1-cos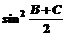 .
.
(1)求角A的大小;
(2)若a=6,则当△ABC面积取最大值时,判断△ABC的形状。
18.(12分)已知函数f(x)=kx+b的图象与x,y轴分别交于点A、B,且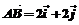 (
( 分别是与x轴、y轴正半轴同向的单位向量),函数g(x)=x2-x-6.
分别是与x轴、y轴正半轴同向的单位向量),函数g(x)=x2-x-6.
(1)求k、b.
(2)当f(x)>g(x)时,求 的最小值。
的最小值。
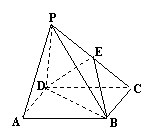 19.(12分)如图,四棱锥P-ABCD中,底面ABCD是正方形,侧面PDC为正三角形,且平面PDC⊥平面ABCD,E为PC的中点.
19.(12分)如图,四棱锥P-ABCD中,底面ABCD是正方形,侧面PDC为正三角形,且平面PDC⊥平面ABCD,E为PC的中点.
(1)求底PA∥平面EDB.
(2)求证:平面EDB⊥平面PBC.
20.(12分)已知函数f(x)=x2-4ax+a2(a<0)
(1)若关于x的不等式f(x)≥x的解集为R,求实数a的最大值;
(2)设函数g(x)=2x2+3af(x),如果g(x)在区间(0,1)上有极小值,求实数a的取值范围。
21.(14分)设数列{an}的首项a1=1,前n项和Sn满足3tSn-(2t+3)Sn-1=3t(t>0,n=2,3,…).
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比为f(t),作数列{bn},b1=1,bn=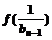 (n=2,3,…),求{bn}的通项bn;
(n=2,3,…),求{bn}的通项bn;
22.(12分)已知动点M在y轴右侧,M到点(0,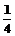 )的距离比它到直线y=-
)的距离比它到直线y=-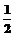 的距离小
的距离小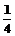 .
.
(1)求动点M轨迹C的方程。
(2)设M、N是轨迹C上相异两点,OM、ON的倾斜角分别为θ1、θ2,当θ1、θ2变化且θ1+θ2为定值θ时,证明直线MN恒过定点,并求出该定点的坐标。




