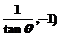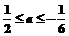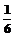17.(12分)在△ABC中,a、b、c分别是角A、B、C的对边,且1-cos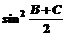 .
.
(1)求角A的大小;
(2)若a=6,则当△ABC面积取最大值时,判断△ABC的形状。
- 答案
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
A
B
C
B
C
D
D
D
C
B
B(文、理)
二、填空题:
13.-1 14.y2=4x(x>0,y>0) 15.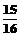 16.
16.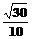 16.(文)
16.(文)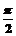
三、解答题:(理科)
17.解:(1)由已知1-(2cos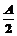
∴2cos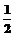 或cosA=-1(舍去)
或cosA=-1(舍去)
∴A=60°
(2)S△=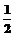 bcsin60°=
bcsin60°=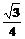 bc
bc
由余弦定理cos60°=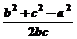
∴b2+c2=bc+36
由b2+c2≥2bc ∴bc≤36
∴S△==9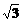 ,此时b=c故△ABC为等边三角形
,此时b=c故△ABC为等边三角形
18.解:(1)设A(-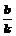 ,0),B(0,b)
,0),B(0,b)
∴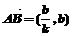 又
又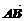 =(2,2)
=(2,2)
∴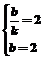 解得
解得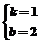
(2)由x+2>x2-x-6 得-2<x<4
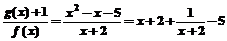 ,由于x+2>0
,由于x+2>0
∴由均值不等式得原式最小值为-3,仅当x=-1时
19.解:(1)证明:连AC交BD于O,连EO
∵E、O分别是中点,
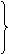 EO∥PA
EO∥PA
∴ EO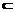 面EDB
面EDB 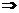 PA∥面EDB
PA∥面EDB
PA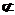 面EDB
面EDB
(2) ∵△PDC为正△
∴DE⊥PC
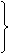 面PDC⊥面ABCD
面PDC⊥面ABCD
BC⊥CD 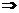 BC⊥DE
BC⊥DE
BC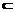 面ABCD
面ABCD
|

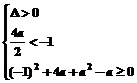
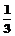 ≤a≤0或a≤
≤a≤0或a≤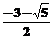
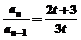 ,又
,又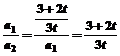
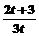 为公比的等比数列
为公比的等比数列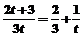
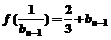
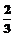 为公差的等差数列
为公差的等差数列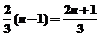
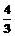 (b2+b4+…b2n)
(b2+b4+…b2n)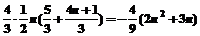
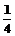 )距离与它到y=-
)距离与它到y=-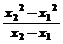 (x-x1),其中tanθ=
(x-x1),其中tanθ=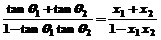
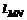 :y=(x1+x2)(x+
:y=(x1+x2)(x+ )-1,所以直线过定点(-
)-1,所以直线过定点(-