
科目: 来源: 题型:
【题目】我国法定劳动年龄是![]() 周岁至退休年龄(退休年龄一般指男
周岁至退休年龄(退休年龄一般指男![]() 周岁,女干部身份
周岁,女干部身份![]() 周岁,女工人
周岁,女工人![]() 周岁).为更好了解我国劳动年龄人口变化情况,有关专家统计了
周岁).为更好了解我国劳动年龄人口变化情况,有关专家统计了![]() 年我国劳动年龄人口和
年我国劳动年龄人口和![]() 周岁人口数量(含预测),得到下表:
周岁人口数量(含预测),得到下表:
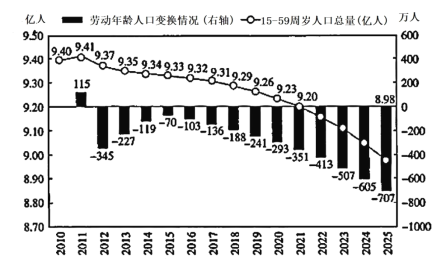
其中![]() 年劳动年龄人口是
年劳动年龄人口是![]() 亿人,则下列结论不正确的是( )
亿人,则下列结论不正确的是( )
A.![]() 年劳动年龄人口比
年劳动年龄人口比![]() 年减少了
年减少了![]() 万人以上
万人以上
B.![]() 这
这![]() 年
年![]() 周岁人口数的平均数是
周岁人口数的平均数是![]() 亿
亿
C.![]() 年,
年,![]() 周岁人口数每年的减少率都小于同年劳动人口每年的减少率
周岁人口数每年的减少率都小于同年劳动人口每年的减少率
D.![]() 年这
年这![]() 年
年![]() 周岁人口数的方差小于这
周岁人口数的方差小于这![]() 年劳动人口数的方差
年劳动人口数的方差
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正四面体![]() 底面的中心为
底面的中心为![]() ,
,![]() 的重心为
的重心为![]() .
.![]() 是
是![]() 内部一动点(包括边界),满足
内部一动点(包括边界),满足![]() ,
,![]() ,
,![]() 不共线且点
不共线且点![]() 到点
到点![]() 的距离与到平面
的距离与到平面![]() 的距离相等.
的距离相等.
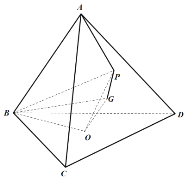
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求四面体
,求四面体![]() 体积的最大值.
体积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】海面上漂浮着![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 七个岛屿,岛与岛之间都没有桥连接,小昊住在
七个岛屿,岛与岛之间都没有桥连接,小昊住在![]() 岛,小皓住在
岛,小皓住在![]() 岛.现政府计划在这七个岛之间建造
岛.现政府计划在这七个岛之间建造![]() 座桥(每两个岛之间至多建造一座桥).若
座桥(每两个岛之间至多建造一座桥).若![]() ,则桥建完后,小吴和小皓可以往来的概率为______;若
,则桥建完后,小吴和小皓可以往来的概率为______;若![]() ,则桥建完后,小昊和小皓可以往来的概率为______.
,则桥建完后,小昊和小皓可以往来的概率为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】设实数列![]() 满足
满足![]() ,则下面说法正确的是( )
,则下面说法正确的是( )
A.若![]() ,则
,则![]() 前2019项中至少有1010个值相等
前2019项中至少有1010个值相等
B.若![]() ,则当
,则当![]() 确定时,一定存在实数
确定时,一定存在实数![]() 使
使![]() 恒成立
恒成立
C.若![]() ,
,![]() 一定为等比数列
一定为等比数列
D.若![]() ,则当
,则当![]() 确定时,一定存在实数
确定时,一定存在实数![]() 使
使![]() 恒成立
恒成立
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙、丙三人独立地对某一技术难题进行攻关.甲能攻克的概率为![]() ,乙能攻克的概率为
,乙能攻克的概率为![]() ,丙能攻克的概率为
,丙能攻克的概率为![]() .
.
(1)求这一技术难题被攻克的概率;
(2)现假定这一技术难题已被攻克,上级决定奖励![]() 万元.奖励规则如下:若只有一人攻克,则此人获得全部奖金
万元.奖励规则如下:若只有一人攻克,则此人获得全部奖金![]() 万元;若只有两人攻克,则奖金奖给此二人,每人各得
万元;若只有两人攻克,则奖金奖给此二人,每人各得![]() 万元;若三人均攻克,则奖金奖给此三人,每人各得
万元;若三人均攻克,则奖金奖给此三人,每人各得![]() 万元.设乙、丙两人得到的奖金数的和为X,求X的分布列和均值.
万元.设乙、丙两人得到的奖金数的和为X,求X的分布列和均值.
查看答案和解析>>
科目: 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】设数组![]() ,
,![]() ,
,![]()
![]() ,数
,数![]() 称为数组
称为数组![]() 的元素.对于数组
的元素.对于数组![]() ,规定:
,规定:
①数组![]() 中所有元素的和为
中所有元素的和为![]() ;
;
②变换![]() ,
,![]() 将数组
将数组![]() 变换成数组
变换成数组![]() ,其中
,其中![]() 表示不超过
表示不超过![]() 的最大整数;
的最大整数;
③若数组![]() ,则当且仅当
,则当且仅当![]()
![]() 时,
时,![]() .
.
如果对数组![]() 中任意
中任意![]() 个元素,存在一种分法,可将其分为两组,每组
个元素,存在一种分法,可将其分为两组,每组![]() 个元素,使得两组所有元素的和相等,则称数组
个元素,使得两组所有元素的和相等,则称数组![]() 具有性质
具有性质![]() .
.
(Ⅰ)已知数组![]() ,
,![]() ,计算
,计算![]() ,
,![]() ,并写出数组
,并写出数组![]() 是否具有性质
是否具有性质![]() ;
;
(Ⅱ)已知数组![]() 具有性质
具有性质![]() ,证明:
,证明:![]() 也具有性质
也具有性质![]() ;
;
(Ⅲ)证明:数组![]() 具有性质
具有性质![]() 的充要条件是
的充要条件是![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com