【题目】已知集合A={x| ![]() >0},集合B={x|y=lg(﹣x2+3x+28)},集合C={x|m+1≤x≤2m﹣1}.
>0},集合B={x|y=lg(﹣x2+3x+28)},集合C={x|m+1≤x≤2m﹣1}.
(1)求(RA)∩B;
(2)若B∪C=B,求实数m的取值范围.
参考答案:
【答案】
(1)解:集合A={x| ![]() >0}={x|x>7或x<﹣2},
>0}={x|x>7或x<﹣2},
B={x|y=lg(﹣x2+3x+28)}={x|﹣4<x<7},
所以RA={x|﹣2≤x≤7}
所以(RA)∩B=[﹣2,7)
(2)解:因为B∪C=B,所以CB
①当C=时,m+1>2m﹣1,即m<2,此时BA
②当C≠时,  ,即2≤m<4,此时BA
,即2≤m<4,此时BA
综上所述,m的取值范围是{m|m<4}
【解析】(1)利用分式不等式的解法求出集合A,函数的定义域求出集合B,求出A的补集,即可求解结果.(2)利用并集关系,转化为子集关系,求解m即可.
【考点精析】利用交、并、补集的混合运算对题目进行判断即可得到答案,需要熟知求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个边长为
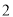 的正三角形和半圆组成的图形,现把
的正三角形和半圆组成的图形,现把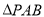 沿直线AB折起使得与圆所在平面垂直,已知点C是半圆的一个三等分点(靠左边一点),点E是线段PB上的点,(1)当点E是PB的中点时,在圆弧上找一点Q,使得
沿直线AB折起使得与圆所在平面垂直,已知点C是半圆的一个三等分点(靠左边一点),点E是线段PB上的点,(1)当点E是PB的中点时,在圆弧上找一点Q,使得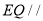 平面
平面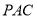 ;(2)当二面角
;(2)当二面角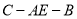 的正切值为
的正切值为 时,求BE的长。
时,求BE的长。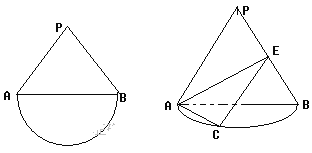
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  (
( 为自然对数的底数).
为自然对数的底数).(1)讨论函数
 的单调性;
的单调性;(2)当
 时,
时,  恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
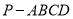 中,底面
中,底面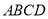 是直角梯形,
是直角梯形, 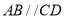 ,
, 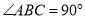 ,
, 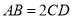 ,
, 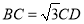 ,
, 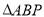 是等边三角形,且侧面
是等边三角形,且侧面 底面
底面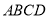 ,
, 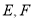 分别是
分别是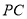 ,
, 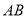 的中点.
的中点.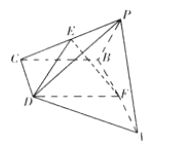
(Ⅰ)求证:
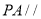 平面
平面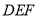 ;
;(Ⅱ)求平面
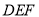 与平面
与平面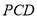 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
 中,
中,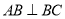 ,
,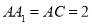 ,
, ,
,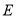 ,
,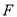 分别是
分别是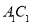 ,
,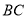 的中点.
的中点.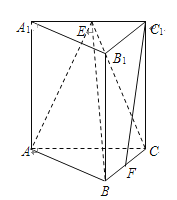
(Ⅰ)求证:平面
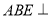 平面
平面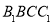 ;
;(Ⅱ)求证:
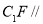 平面
平面 ;
;(Ⅲ)求三棱锥
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A={x|(2x)2﹣62x+8≤0},函数f(x)=log2x(x∈A).
(1)求函数f(x)的定义域;
(2)若函数h(x)=[f(x)]2﹣log2(2x),求函数h(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如下图:

(1)记事件
 为:“从这批小龙虾中任取一只,重量不超过35
为:“从这批小龙虾中任取一只,重量不超过35 的小龙虾”,求
的小龙虾”,求 的估计值;
的估计值;(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
等级
一等品
二等品
三等品
重量(
 )
)


按分层抽样抽取10只,再随机抽取3只品尝,记
 为抽到二等品的数量,求抽到二级品的期望.
为抽到二等品的数量,求抽到二级品的期望.
相关试题

