【题目】某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如下图:

(1)记事件![]() 为:“从这批小龙虾中任取一只,重量不超过35
为:“从这批小龙虾中任取一只,重量不超过35![]() 的小龙虾”,求
的小龙虾”,求![]() 的估计值;
的估计值;
(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量( |
|
|
|
按分层抽样抽取10只,再随机抽取3只品尝,记![]() 为抽到二等品的数量,求抽到二级品的期望.
为抽到二等品的数量,求抽到二级品的期望.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)由于![]() 只小龙虾中重量不超过
只小龙虾中重量不超过![]() 的小龙虾有28,可以求得;
的小龙虾有28,可以求得;
(2)从统计图中可以估计每只小龙虾的重量28.5克,即可估算100千克小龙虾的数量;
(3)由题意知抽取一等品、二等品、三等品分别为![]() 只、
只、![]() 只、
只、![]() 只,
只, ![]() 分别求概率,利用期望公式计算期望即可.
分别求概率,利用期望公式计算期望即可.
试题解析:
(1)由于![]() 只小龙虾中重量不超过
只小龙虾中重量不超过![]() 的小龙虾有
的小龙虾有![]() (只)
(只)
所以![]()
(2)从统计图中可以估计每只小龙虾的重量
![]()
![]() (克)
(克)
所以购进![]() 千克,小龙虾的数量约有
千克,小龙虾的数量约有![]() (只)
(只)
(3)由题意知抽取一等品、二等品、三等品分别为![]() 只、
只、![]() 只、
只、![]() 只,
只, ![]()
则可得![]() ,
, ![]()
![]() ,
, ![]()
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|
 >0},集合B={x|y=lg(﹣x2+3x+28)},集合C={x|m+1≤x≤2m﹣1}.
>0},集合B={x|y=lg(﹣x2+3x+28)},集合C={x|m+1≤x≤2m﹣1}.
(1)求(RA)∩B;
(2)若B∪C=B,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
 中,
中,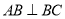 ,
,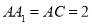 ,
, ,
,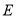 ,
,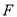 分别是
分别是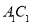 ,
,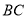 的中点.
的中点.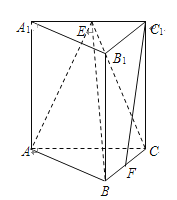
(Ⅰ)求证:平面
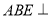 平面
平面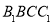 ;
;(Ⅱ)求证:
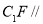 平面
平面 ;
;(Ⅲ)求三棱锥
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A={x|(2x)2﹣62x+8≤0},函数f(x)=log2x(x∈A).
(1)求函数f(x)的定义域;
(2)若函数h(x)=[f(x)]2﹣log2(2x),求函数h(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为G(x)(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)(万元)满足R(x)=
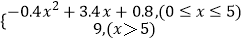 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)要使甲厂有盈利,求产量x的范围;
(3)甲厂生产多少台产品时,可使盈利最多? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=a﹣
 为奇函数.
为奇函数.
(1)求a的值;
(2)试判断函数f(x)在(﹣∞,+∞)上的单调性,并证明你的结论;
(3)若对任意的t∈R,不等式f[t2﹣(m﹣2)t]+f(t2﹣m+1)>0恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的取值范围.
相关试题

