【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且
,且![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(点
两点(点![]() 均在第一象限),且直线
均在第一象限),且直线![]() 的斜率成等比数列,证明:直线
的斜率成等比数列,证明:直线![]() 的斜率为定值.
的斜率为定值.
参考答案:
【答案】(1) ![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:
(1)根据椭圆的离心率和所过的点得到关于![]() 的方程组,解得
的方程组,解得![]() 后可得椭圆的方程.(2)由题意设直线
后可得椭圆的方程.(2)由题意设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立后消元可得二次方程,根据二次方程根与系数的关系可得直线
,与椭圆方程联立后消元可得二次方程,根据二次方程根与系数的关系可得直线![]() 的斜率,再根据题意可得
的斜率,再根据题意可得![]() ,根据此式可求得
,根据此式可求得![]() ,为定值.
,为定值.
试题解析:
(1)由题意可得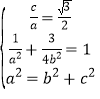 ,解得
,解得![]() .
.
故椭圆![]() 的方程为
的方程为![]() .
.
(2)由题意可知直线![]() 的斜率存在且不为0,设直线
的斜率存在且不为0,设直线![]() 的方程为
的方程为![]() ,
,
由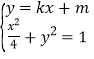 ,消去
,消去![]() 整理得
整理得![]() ,
,
∵直线![]() 与椭圆交于两点,
与椭圆交于两点,
∴![]() .
.
设点![]() 的坐标分别为
的坐标分别为![]() ,
,
则![]() ,
,
∴![]() .
.
∵直线![]() 的斜率成等比数列,
的斜率成等比数列,
∴![]() ,
,
整理得![]() ,
,
∴![]() ,
,
又![]() ,所以
,所以![]() ,
,
结合图象可知![]() ,故直线
,故直线![]() 的斜率为定值.
的斜率为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C的极坐标方程是ρ=2sinθ,直线l的参数方程是
 (t为参数).设直线l与x轴的交点是M,N是曲线C上一动点,求MN的最大值.
(t为参数).设直线l与x轴的交点是M,N是曲线C上一动点,求MN的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3.D是线段BC的中点.

(1)求直线DB1与平面A1C1D所成角的正弦值;
(2)求二面角B1﹣A1D﹣C1的大小的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,底面
 是边长为3的正方形,
是边长为3的正方形, 平面
平面 ,
, ,
, ,
, 与平面
与平面 所成的角为
所成的角为 .
.
(1)求证:平面
 平面
平面 ;
;(2)求二面角
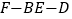 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)设
 ,若不等式
,若不等式 对任意
对任意 恒成立,求
恒成立,求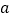 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知非空集合M满足M{0,1,2,…,n}(n≥2,n∈N+).若存在非负整数k(k≤n),使得当a∈M时,均有2k﹣a∈M,则称集合M具有性质P.设具有性质P的集合M的个数为f(n).
(1)求f(2)的值;
(2)求f(n)的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,已知圆
 的圆心坐标为
的圆心坐标为 ,半径为
,半径为 ,以坐标原点为极点,
,以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,直线l的参数方程为:
轴的正半轴为极轴建立极坐标系,直线l的参数方程为: (
( 为参数).
为参数).(1)求圆
 和直线l的极坐标方程;
和直线l的极坐标方程;(2)点
 的极坐标为
的极坐标为 ,直线l与圆
,直线l与圆 相交于A,B,求
相交于A,B,求 的值.
的值.
相关试题

