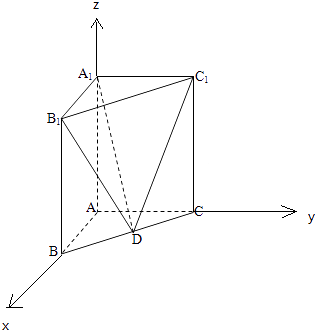
【题目】如图,在直三棱柱ABC﹣A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3.D是线段BC的中点. 
(1)求直线DB1与平面A1C1D所成角的正弦值;
(2)求二面角B1﹣A1D﹣C1的大小的余弦值.
参考答案:
【答案】
(1)解:因为在直三棱柱ABC﹣A1B1C1中,AB⊥AC,
所以分别以AB、AC、AA1所在的直线为x轴、y轴、z轴,建立空间直角坐标系,
则A(0,0,0),B(2,0,0),C(0,4,0),A1(0,0,3),B1(2,0,3),C1(0,4,3),
因为D是BC的中点,所以D(1,2,0),
因为 ![]() ,设平面A1C1D的法向量
,设平面A1C1D的法向量 ![]() ,
,
则 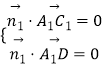 ,即
,即 ![]() ,取
,取 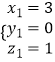 ,
,
所以平面A1C1D的法向量 ![]() ,而
,而 ![]() ,
,
所以 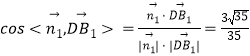 ,
,
所以直线DB1与平面A1C1D所成角的正弦值为 ![]()
(2)解: ![]() ,
, ![]() ,
,
设平面B1A1D的法向量 ![]() ,
,
则 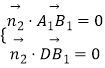 ,即
,即 ![]() ,
,
取  ,平面B1A1D的法向量
,平面B1A1D的法向量 ![]() ,
,
所以 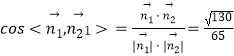 ,
,
二面角B1﹣A1D﹣C1的大小的余弦值 ![]() .
.
【解析】(1)分别以AB、AC、AA1所在的直线为x轴、y轴、z轴,建立空间直角坐标系,利用向量法能求出直线DB1与平面A1C1D所成角的正弦值.(2)求出平面B1A1D的法向量和平面B1A1D的法向量,利用向量法能求出二面角B1﹣A1D﹣C1的大小的余弦值.
【考点精析】根据题目的已知条件,利用空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则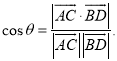 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ,直线y=
,直线y=  x为曲线y=f(x)的切线(e为自然对数的底数).
x为曲线y=f(x)的切线(e为自然对数的底数).
(1)求实数a的值;
(2)用min{m,n}表示m,n中的最小值,设函数g(x)=min{f(x),x﹣ }(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
}(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修:4﹣2:矩阵与变换
若圆C:x2+y2=1在矩阵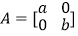 (a>0,b>0)对应的变换下变成椭圆E:
(a>0,b>0)对应的变换下变成椭圆E:  ,求矩阵A的逆矩阵A﹣1 .
,求矩阵A的逆矩阵A﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C的极坐标方程是ρ=2sinθ,直线l的参数方程是
 (t为参数).设直线l与x轴的交点是M,N是曲线C上一动点,求MN的最大值.
(t为参数).设直线l与x轴的交点是M,N是曲线C上一动点,求MN的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,底面
 是边长为3的正方形,
是边长为3的正方形, 平面
平面 ,
, ,
, ,
, 与平面
与平面 所成的角为
所成的角为 .
.
(1)求证:平面
 平面
平面 ;
;(2)求二面角
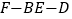 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,且
,且 过点
过点 .
.(1)求椭圆
 的方程;
的方程;(2)若直线
 与椭圆
与椭圆 交于
交于 两点(点
两点(点 均在第一象限),且直线
均在第一象限),且直线 的斜率成等比数列,证明:直线
的斜率成等比数列,证明:直线 的斜率为定值.
的斜率为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)设
 ,若不等式
,若不等式 对任意
对任意 恒成立,求
恒成立,求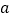 的取值范围.
的取值范围.
相关试题

