【题目】已知非空集合M满足M{0,1,2,…,n}(n≥2,n∈N+).若存在非负整数k(k≤n),使得当a∈M时,均有2k﹣a∈M,则称集合M具有性质P.设具有性质P的集合M的个数为f(n).
(1)求f(2)的值;
(2)求f(n)的表达式.
参考答案:
【答案】
(1)解:当n=2时,M={0},{1},{2},{0,2},{0,1,2}具有性质P,
对应的k分别为0,1,2,1,1,故f(2)=5.
(2)解:可知当n=k时,具有性质P的集合M的个数为f(t),
则当n=k+1时,f(t+1)=f(t)+g(t+1),
其中g(t+1)表达t+1∈M也具有性质P的集合M的个数,
下面计算g(t+1)关于t的表达式,
此时应有2k≥t+1,即 ![]() ,故对n=t分奇偶讨论,
,故对n=t分奇偶讨论,
①当t为偶数时,t+1为奇数,故应该有 ![]() ,
,
则对每一个k,t+1和2k﹣t﹣1必然属于集合M,且t和2k﹣t,…,k和k共有t+1﹣k组数,每一组数中的两个数必然同时属于或不属于集合M,
故对每一个k,对应的具有性质P的集合M的个数为 ![]() ,
,
所以 ![]() ,
,
②当t为奇数时,t+1为偶数,故应该有 ![]() ,
,
同理 ![]() ,
,
综上,可得 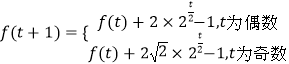 又f(2)=5,
又f(2)=5,
由累加法解得 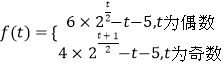
即 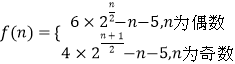
【解析】(1)当n=2时,M={0},{1},{2},{0,2},{0,1,2}具有性质P,求出对应的k,即可得出.(2)可知当n=k时,具有性质P的集合M的个数为f(t),当n=k+1时,f(t+1)=f(t)+g(t+1),其中g(t+1)表达t+1∈M也具有性质P的集合M的个数,
计算g(t+1)关于t的表达式,此时应有2k≥t+1,即 ![]() ,故对n=t分奇偶讨论,利用集合M具有性质P即可得出.
,故对n=t分奇偶讨论,利用集合M具有性质P即可得出.
【考点精析】解答此题的关键在于理解集合的表示方法-特定字母法的相关知识,掌握①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合.③描述法:{![]() |
|![]() 具有的性质},其中
具有的性质},其中![]() 为集合的代表元素.④图示法:用数轴或韦恩图来表示集合.
为集合的代表元素.④图示法:用数轴或韦恩图来表示集合.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,底面
 是边长为3的正方形,
是边长为3的正方形, 平面
平面 ,
, ,
, ,
, 与平面
与平面 所成的角为
所成的角为 .
.
(1)求证:平面
 平面
平面 ;
;(2)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,且
,且 过点
过点 .
.(1)求椭圆
 的方程;
的方程;(2)若直线
 与椭圆
与椭圆 交于
交于 两点(点
两点(点 均在第一象限),且直线
均在第一象限),且直线 的斜率成等比数列,证明:直线
的斜率成等比数列,证明:直线 的斜率为定值.
的斜率为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)设
 ,若不等式
,若不等式 对任意
对任意 恒成立,求
恒成立,求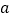 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,已知圆
 的圆心坐标为
的圆心坐标为 ,半径为
,半径为 ,以坐标原点为极点,
,以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,直线l的参数方程为:
轴的正半轴为极轴建立极坐标系,直线l的参数方程为: (
( 为参数).
为参数).(1)求圆
 和直线l的极坐标方程;
和直线l的极坐标方程;(2)点
 的极坐标为
的极坐标为 ,直线l与圆
,直线l与圆 相交于A,B,求
相交于A,B,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】高中生在被问及“家,朋友聚集的地方,个人空间”三个场所中“感到最幸福的场所在哪里?”这个问题时,从中国某城市的高中生中,随机抽取了55人,从美国某城市的高中生中随机抽取了45人进行答题.中国高中生答题情况是:选择家的占
 、朋友聚集的地方占
、朋友聚集的地方占 、个人空间占
、个人空间占 .美国高中生答题情况是:朋友聚集的地方占
.美国高中生答题情况是:朋友聚集的地方占 、家占
、家占 、个人空间占
、个人空间占 .如下表:
.如下表:在家里最幸福
在其它场所幸福
合计
中国高中生
美国高中生
合计
(Ⅰ)请将
 列联表补充完整;试判断能否有
列联表补充完整;试判断能否有 的把握认为“恋家”与否与国别有关;
的把握认为“恋家”与否与国别有关;(Ⅱ)从被调查的不“恋家”的美国学生中,用分层抽样的方法选出4人接受进一步调查,再从4人中随机抽取2人到中国交流学习,求2人中含有在“个人空间”感到幸福的学生的概率.
附:
 ,其中
,其中 .
.
0.050
0.025
0.010
0.001

3.841
5.024
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱锥P﹣ABC中,D为AB的中点.

(1)与BC平行的平面PDE交AC于点E,判断点E在AC上的位置并说明理由如下:
(2)若PA=PB,且△PCD为锐角三角形,又平面PCD⊥平面ABC,求证:AB⊥PC.
相关试题

