【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 和圆
和圆![]() .
.

(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() 是,求直线
是,求直线![]() 的方程;
的方程;
(2)设![]() 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点![]() 的无穷多对互相垂直的直线
的无穷多对互相垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和圆
和圆![]() 相交,且直线
相交,且直线![]() 与被圆
与被圆![]() 截得的弦长与直线
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点
截得的弦长相等,试求所有满足条件的点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() 或点
或点![]() .
.
【解析】
试题分析:(1)直线![]() 过点
过点![]() ,故可以设出直线
,故可以设出直线![]() 的点斜式方程,根据圆的几何性质、点到直线距离公式及勾股定理到一个关于直线斜率
的点斜式方程,根据圆的几何性质、点到直线距离公式及勾股定理到一个关于直线斜率![]() 的方程,解方程求出
的方程,解方程求出![]() 值即可;(2)由于两直线斜率为之积为
值即可;(2)由于两直线斜率为之积为![]() ,可以设出过
,可以设出过![]() 点的直线
点的直线![]() 与
与![]() 的点斜式方程,由直线
的点斜式方程,由直线![]() 被圆
被圆![]() 截得的弦长与直线
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,可以得到一个关于直线斜率的方程,由方程恒成立可得关于
截得的弦长相等,可以得到一个关于直线斜率的方程,由方程恒成立可得关于![]() 的方程组,求得
的方程组,求得![]() 的值即可.
的值即可.
试题解析:(1)由于直线![]() 与圆
与圆![]() 不相交,所以直线
不相交,所以直线![]() 的斜率存在,设
的斜率存在,设
直线![]() 的方程为
的方程为![]() ,圆
,圆![]() 的圆心
的圆心![]() 到直线
到直线![]() 的距离为
的距离为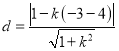 ,
,
∵直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() 或
或![]() ,
,
所以直线![]() 的方程为
的方程为![]() 或
或![]() ;
;
(2)设点![]() 满足条件,不妨设直线
满足条件,不妨设直线![]() 的方程为
的方程为![]() ,
,
![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,因为
,因为![]() 和
和![]() 的半径相等,
的半径相等,
及直线![]() 被圆
被圆![]() 截得的弦长与直线
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,所以圆
截得的弦长相等,所以圆![]() 的圆心到直线
的圆心到直线![]() 的距离和圆
的距离和圆![]() 的圆心到直线
的圆心到直线![]() 的距离相等,即
的距离相等,即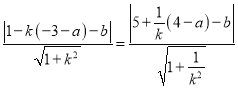 ,
,
整理得:![]() ,
,
∴![]() 或
或![]() ,
,
即![]() 或
或![]() .
.
因为![]() 的取值有无穷多个,所以
的取值有无穷多个,所以
![]() ,或
,或![]() ,解得
,解得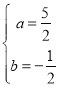 或
或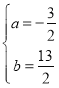 ,
,
这样点![]() 只可能是点
只可能是点![]() 或点
或点![]() ,经检验点
,经检验点![]() 和
和![]() 满足题目条件.
满足题目条件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】庆华租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】假设我国发射的天宫一号飞行器需要建造隔热层.已知天宫一号建造的隔热层必须使用20年,每厘米厚的隔热层建造成本是6万元,天宫一号每年的能源消耗费用H(万元)与隔热层厚度
 (厘米)满足关系式:
(厘米)满足关系式: (当
(当 时表示无隔热层),若无隔热层,则每年能源消耗费用为8万元.设
时表示无隔热层),若无隔热层,则每年能源消耗费用为8万元.设 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和. (I)求
 的值和
的值和 的表达式;
的表达式; (II)当隔热层修建多少厘米厚时,总费用
 最小,并求出最小值.
最小,并求出最小值. -
科目: 来源: 题型:
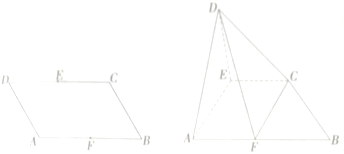
查看答案和解析>>【题目】如图,四边形
 是边长为2的菱形,
是边长为2的菱形,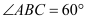 ,E,F分别为
,E,F分别为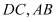 的中点,将
的中点,将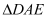 沿
沿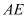 折起,使得
折起,使得 .
.
(1)求证:平面
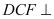 平面
平面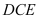 ;
;(2)求二面角
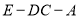 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了判断高中三年级学生选修文理科是否与性别有关,现随机抽取50名学生,得到2×2列联表:
理科
文科
总计
男
13
10
23
女
7
20
27
总计
20
30
50
已知P(K2≥3.841)≈0.05,P(K2≥5.024)≈0.025.根据表中数据,得到K2≈4.844,则认为选修文理科与性别有关系出错的可能性约为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校做了一次关于“感恩父母”的问卷调查,从8~10岁,11~12岁,13~14岁,15~16岁四个年龄段回收的问卷依次为:120份,180份,240份,x份.因调查需要,从回收的问卷中按年龄段分层抽取容量为300的样本,其中在11~12岁学生问卷中抽取60份,则在15~16岁学生中抽取的问卷份数为( )
A.60 B.80 C.120 D.180
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)讨论函数
 的单调性;
的单调性;(2)若
 ,设
,设
 ,若对任意
,若对任意
 ,
, 恒成立,求实数
恒成立,求实数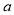 的取值范围.
的取值范围.
相关试题

