【题目】某校做了一次关于“感恩父母”的问卷调查,从8~10岁,11~12岁,13~14岁,15~16岁四个年龄段回收的问卷依次为:120份,180份,240份,x份.因调查需要,从回收的问卷中按年龄段分层抽取容量为300的样本,其中在11~12岁学生问卷中抽取60份,则在15~16岁学生中抽取的问卷份数为( )
A.60 B.80 C.120 D.180
参考答案:
【答案】C
【解析】从11~12岁的学生中回收180份问卷,从中抽取60份,则抽样比为![]() .
.
∵从回收的问卷中按年龄段分层抽取容量为300的样本,
∴从8~10岁,11~12岁,13~14岁,15~16岁四个年龄段回收的问卷总数为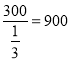 (份),则15~16岁回收问卷份数为x=900-120-180-240=360(份).
(份),则15~16岁回收问卷份数为x=900-120-180-240=360(份).
∴在15~16岁学生中抽取的问卷份数为360×![]() =120(份),故选C.
=120(份),故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是边长为2的菱形,
是边长为2的菱形,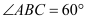 ,E,F分别为
,E,F分别为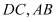 的中点,将
的中点,将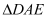 沿
沿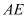 折起,使得
折起,使得 .
.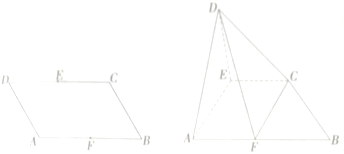
(1)求证:平面
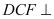 平面
平面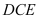 ;
;(2)求二面角
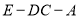 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知圆
中,已知圆 和圆
和圆 .
.
(1)若直线
 过点
过点 ,且被圆
,且被圆 截得的弦长为
截得的弦长为 是,求直线
是,求直线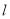 的方程;
的方程;(2)设
 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点 的无穷多对互相垂直的直线
的无穷多对互相垂直的直线 和
和 ,它们分别与圆
,它们分别与圆 和圆
和圆 相交,且直线
相交,且直线 与被圆
与被圆 截得的弦长与直线
截得的弦长与直线 被圆
被圆 截得的弦长相等,试求所有满足条件的点
截得的弦长相等,试求所有满足条件的点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了判断高中三年级学生选修文理科是否与性别有关,现随机抽取50名学生,得到2×2列联表:
理科
文科
总计
男
13
10
23
女
7
20
27
总计
20
30
50
已知P(K2≥3.841)≈0.05,P(K2≥5.024)≈0.025.根据表中数据,得到K2≈4.844,则认为选修文理科与性别有关系出错的可能性约为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)讨论函数
 的单调性;
的单调性;(2)若
 ,设
,设
 ,若对任意
,若对任意
 ,
, 恒成立,求实数
恒成立,求实数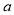 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种植物生长发育的数量y与时间x的关系如下表:
x
1
2
3
…
y
1
3
8
…
则下面的函数关系式中,能表达这种关系的是( )
A.y=2x-1 B.y=x2-1
C.y=2x-1 D.y=1.5x2-2.5x+2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 :方程
:方程 有两个不等的负根;
有两个不等的负根;  :方程
:方程 无实根.若“
无实根.若“ 或
或 ”为真,“
”为真,“ 且
且 ”为假,求
”为假,求 的取值范围.
的取值范围.
相关试题

