【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
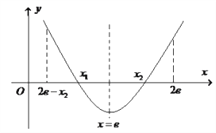
(2) 若函数![]() 有两个零点
有两个零点![]() ,
, ![]()
![]() ,且
,且![]() ,证明:
,证明: ![]() .
.
参考答案:
【答案】(1)当![]() 时,知
时,知![]() 在
在![]() 上递减;当
上递减;当![]() 时,
时, ![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;(2)证明见解析.
上递增;(2)证明见解析.
【解析】
试题分析:
(1)由函数的解析式了的![]() ,
, ![]() ,分类讨论有:当
,分类讨论有:当![]() 时,知
时,知![]() 在
在![]() 上递减;当
上递减;当![]() 时,
时, ![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
(2)由(1)知, ![]() ,
, ![]() ,且
,且 ![]() , 故
, 故![]() ,
, ![]() ,原问题等价于
,原问题等价于![]() ,结合单调性转化为
,结合单调性转化为![]() 即可,而
即可,而![]() ,
, ![]() ,构造函数,令
,构造函数,令![]() ,
, ![]() ,结合导函数的性质可得
,结合导函数的性质可得![]() ,即
,即![]() ,则结论得证.
,则结论得证.
试题解析:
(1)![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() ,知
,知![]() 在
在![]() 上是递减的;
上是递减的;
当![]() 时,
时, ![]() ,知
,知![]() 在
在![]() 上是递减的,在
上是递减的,在![]() 上递增的.
上递增的.
(2)由(1)知, ![]() ,
, ![]() ,
,
依题意![]() ,即
,即![]() ,
,
由![]() 得,
得, ![]() ,
, ![]() ,
, ![]() ,
,
由![]() 及
及![]() 得,
得, ![]() ,即
,即![]() ,
,
欲证![]() ,只要
,只要![]() ,
,
注意到![]() 在
在![]() 上是递减的,且
上是递减的,且![]() ,
,
只要证明![]() 即可,
即可,
由![]() 得
得![]() ,
,
所以![]()
![]()
![]()
![]() ,
, ![]() ,
,
令![]() ,
, ![]() ,
,
则![]() ,知
,知![]() 在
在![]() 上是递增的,于是
上是递增的,于是![]() ,即
,即
![]() ,综上,
,综上, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家拟在2020年举行促销活动,经调查测算,某产品的年销售量(即该厂的年产量)
 万件与年促销费用
万件与年促销费用 万元,满足
万元,满足 (
( 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2020年生产该产品的固定投入为8万元,每生产1万件,该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2020年生产该产品的固定投入为8万元,每生产1万件,该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).(1)将2020年该产品的利润
 (万元)表示为年促销费用
(万元)表示为年促销费用 (万元)的函数;
(万元)的函数;(2)该厂家2020年的促销费用投入多少万元时,厂家的利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县共有90间农村淘宝服务站,随机抽取5间,统计元旦期间的网购金额(单位:万元)的茎叶图如图所示,其中茎为十位数,叶为个位数.
(1)根据茎叶图计算样本均值;
(2)若网购金额(单位:万元)不小于18的服务站定义为优秀服务站,其余为非优秀服务站.根据茎叶图推断90间服务站中有几间优秀服务站?
(3)从随机抽取的5间服务站中再任取2间作网购商品的调查,求恰有1间是优秀服务站的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在多面体
 中,底面
中,底面 是梯形,四边形
是梯形,四边形 是正方形,
是正方形,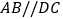 ,
,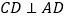 ,面
,面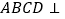 面
面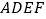 ,
,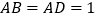 .
.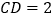 .
.(1)求证:平面
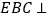 平面
平面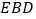 ;
;(2)设
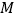 为线段
为线段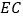 上一点,
上一点,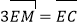 ,试问在线段
,试问在线段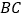 上是否存在一点
上是否存在一点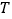 ,使得
,使得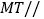 平面
平面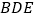 ,若存在,试指出点
,若存在,试指出点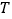 的位置;若不存在,说明理由?
的位置;若不存在,说明理由?(3)在(2)的条件下,求点
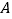 到平面
到平面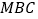 的距离.
的距离.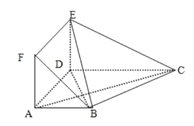
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 的底面
的底面 为直角梯形,
为直角梯形, ,
, ,
, ,
, 为正三角形.
为正三角形.
(1)若点
 是棱
是棱 的中点,求证:
的中点,求证: 平面
平面 ;
;(2)若平面
 ⊥平面
⊥平面 ,在(1)的条件下,试求四棱锥
,在(1)的条件下,试求四棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 ,且直线
,且直线 经过曲线
经过曲线 的左焦点
的左焦点 .
.(1)求
 的值及直线
的值及直线 的普通方程;
的普通方程;(2)设曲线
 的内接矩形的周长为
的内接矩形的周长为 ,求
,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 .
.(1)若函数
 在
在 处取得极值,求实数
处取得极值,求实数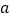 的值;
的值;(2)在(1)的结论下,若关于
 的不等式
的不等式 ,当
,当 时恒成立,求
时恒成立,求 的值;
的值;(3)令
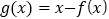 ,若关于
,若关于 的方程
的方程 在
在 内至少有两个解,求出实数
内至少有两个解,求出实数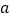 的取值范围。
的取值范围。
相关试题

