【题目】已知椭圆![]() 的一个焦点与上、下顶点构成直角三角形,以椭圆
的一个焦点与上、下顶点构成直角三角形,以椭圆![]() 的长轴长为直径的圆与直线
的长轴长为直径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点且不平行于![]() 轴的动直线与椭圆
轴的动直线与椭圆![]() 相交于
相交于![]() 两点,探究在
两点,探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,试求出定值和点
为定值?若存在,试求出定值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)定点为
;(2)定点为![]() .
.
【解析】试题分析:(1)由椭圆几何意义得![]() ,再根据圆心到切线距离等于半径得
,再根据圆心到切线距离等于半径得![]() ,解得
,解得![]() ,
, ![]() (2)先根据向量数量积化简
(2)先根据向量数量积化简![]() ,再联立直线方程与椭圆方程,利用韦达定理代人化简得
,再联立直线方程与椭圆方程,利用韦达定理代人化简得![]() ,最后根据k的任意性确定点
,最后根据k的任意性确定点![]() 的坐标及定值
的坐标及定值
试题解析:(1)由题意知, 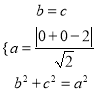 ,解得
,解得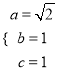 ,
,
则椭圆![]() 的方程为
的方程为![]() .
.
(2)当直线的斜率存在时,设直线![]() ,
,
联立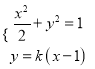 ,得
,得![]() ,
,
∴![]() .
.
假设![]() 轴上存在定点
轴上存在定点![]() ,使得
,使得![]() 为定值,
为定值,
∴![]()
![]()
![]()
![]() .
.
要使![]() 为定值,则
为定值,则![]() 的值与
的值与![]() 无关,∴
无关,∴![]() ,
,
解得![]() ,此时
,此时![]() 为定值,定点为
为定值,定点为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆C:
 =1(a>b>0)过点(0,4),离心率为
=1(a>b>0)过点(0,4),离心率为  .
.
(1)求椭圆C的方程;
(2)求过点(3,0)且斜率为 的直线被椭圆所截得线段的中点坐标.
的直线被椭圆所截得线段的中点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1 , ∠BAA1=60°.
(Ⅰ)证明:AB⊥A1C;
(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”近年来成为了百姓耳熟能详的热门词汇,对于旅游业来说,“一带一路”战略的提出,让“丝路之旅”超越了旅游产品、旅游线路的简单范畴,赋予了旅游促进跨区域融合的新理念. 而其带来的设施互通、经济合作、人员往来、文化交融更是将为相关区域旅游发展带来巨大的发展机遇.为此,旅游企业们积极拓展相关线路;各地旅游主管部门也在大力打造丝路特色旅游品牌和服务.某市旅游局为了解游客的情况,以便制定相应的策略. 在某月中随机抽取甲、乙两个景点10天的游客数,统计得到茎叶图如下:

(1)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据,以每天游客人数频率作为概率.今从这段时期内任取4天,记其中游客数超过130人的天数为
 ,求概率
,求概率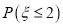 ;
;(2)现从上图20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于125且不高于135人的天数为
 ,求
,求 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线
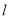 经过点
经过点 ,倾斜角为
,倾斜角为 .在以原点为极点,
.在以原点为极点,  轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 的方程为
的方程为 .
.(1)写出直线
 的参数方程和曲线
的参数方程和曲线 的直角坐标方程;
的直角坐标方程;(2)设直线
 与曲线
与曲线 相交于
相交于 两点,求
两点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣(2m+1)x+2m(m∈R).
(1)当m=1时,解关于x的不等式xf(x)≤0;
(2)解关于x的不等式f(x)>0. -
科目: 来源: 题型:
查看答案和解析>>【题目】正数数列{an}的前n项和为Sn , 已知对于任意的n∈Z+ , 均有Sn与1正的等比中项等于an与1的等差中项.
(1)试求数列{an}的通项公式;
(2)设bn=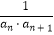 ,数列{bn}的前n项和为Tn , 求证:Tn<
,数列{bn}的前n项和为Tn , 求证:Tn<  .
.
相关试题

