【题目】正数数列{an}的前n项和为Sn , 已知对于任意的n∈Z+ , 均有Sn与1正的等比中项等于an与1的等差中项.
(1)试求数列{an}的通项公式;
(2)设bn= ![]() ,数列{bn}的前n项和为Tn , 求证:Tn<
,数列{bn}的前n项和为Tn , 求证:Tn< ![]() .
.
参考答案:
【答案】
(1)解:由题意得: ![]() ,故
,故 ![]() …①,又
…①,又 ![]() …②,
…②,
②﹣①得: ![]() ,整理得:(an+1+an)(an+1﹣an﹣2)=0.
,整理得:(an+1+an)(an+1﹣an﹣2)=0.
由已知an>0,∴an+1+an>0,故an+1﹣an﹣2=0,
即an+1﹣an=2,所以数列{an}为公差d=2的等差数列.
又由 ![]() 可得:a1=1,∴an=1+(n﹣1)2=2n﹣1
可得:a1=1,∴an=1+(n﹣1)2=2n﹣1
(2)解:由题意可得 ![]() ,
,
∴Tn=b1+b2+…+bn= ![]() [1﹣
[1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() =
= ![]() [1﹣
[1﹣ ![]() ]<
]< ![]()
【解析】(1)由条件等差中项、等比中项的定义,求得:an+1﹣an=2,可得数列{an}为公差d=2的等差数列,再结合a1=1,求得{an}的通项公式.(2)先化简数列{bn}的通项公式,再利用裂项法求得它的前n项和,可得结论.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的一个焦点与上、下顶点构成直角三角形,以椭圆
的一个焦点与上、下顶点构成直角三角形,以椭圆 的长轴长为直径的圆与直线
的长轴长为直径的圆与直线 相切.
相切.(1)求椭圆
 的标准方程;
的标准方程;(2)设过椭圆右焦点且不平行于
 轴的动直线与椭圆
轴的动直线与椭圆 相交于
相交于 两点,探究在
两点,探究在 轴上是否存在定点
轴上是否存在定点 ,使得
,使得 为定值?若存在,试求出定值和点
为定值?若存在,试求出定值和点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线
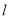 经过点
经过点 ,倾斜角为
,倾斜角为 .在以原点为极点,
.在以原点为极点,  轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 的方程为
的方程为 .
.(1)写出直线
 的参数方程和曲线
的参数方程和曲线 的直角坐标方程;
的直角坐标方程;(2)设直线
 与曲线
与曲线 相交于
相交于 两点,求
两点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣(2m+1)x+2m(m∈R).
(1)当m=1时,解关于x的不等式xf(x)≤0;
(2)解关于x的不等式f(x)>0. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
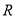 上的函数
上的函数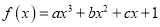 同时满足以下条件:①
同时满足以下条件:①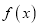 在
在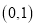 上是减函数,在
上是减函数,在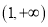 上是增函数;②
上是增函数;②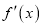 是偶函数;③
是偶函数;③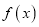 在
在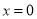 处的切线与直线
处的切线与直线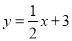 垂直.
垂直.(1)取函数
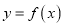 的解析式;
的解析式;(2)设
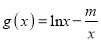 ,若存在实数
,若存在实数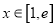 ,使
,使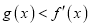 ,求实数
,求实数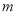 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,B=
 ,AC=2
,AC=2 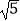 ,cosC=
,cosC= 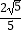 .
. 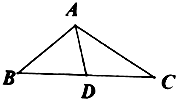
(1)求sin∠BAC的值及BC的长度;
(2)设BC的中点为D,求中线AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.
(Ⅰ)求证:EF∥平面PBC;
(Ⅱ)求二面角E﹣DF﹣A的余弦值;
(Ⅲ)在棱PC上是否存在一点G,使GF⊥平面EDF?若存在,指出点G的位置;若不存在,说明理由.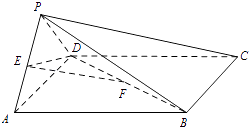
相关试题

