搜索
【题目】(本题共12分）已知函数
(1)讨论
的单调性；
(2)是否存在常数
，使
对任意的
和任意的
都成立，若存在，求出t的取值范围；若不存在，请说明理由．
参考答案：
【答案】（1）详见解析（2）
【解析】试题分析：
(1)首先对函数
求导，结合定义域在
，对参数
小于等于0,和大于0两种情况进行讨论。
(2)恒成立问题,首先求出
在
上的最小值
,再求出
的最小值,从而求出t的范围
试题解析：
（1）
，
①当
时， 
， 
在区间
上单调递减；
②当
时，令
，得
，当
时， 
， 
单调递减；当
时， 
， 
单调递增；
综上所得，当
时， 
在区间
上单调递减；当
时， 
在区间
单调递减， 
在区间
单调递增
（2）
时， 
， 
单调递减；
时， 
， 
单调递增；
又因为
在
单调递减，且
， 
，
存在
， 
，所以当
时， 
， 
单调递增，当
时， 
， 
单调递减，所以
故
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙、丙、丁4名同学被随机地分到A、B、C三个社区参加社会实践，要求每个社区至少有一名同学．
（1）求甲、乙两人都被分到A社区的概率；
（2）求甲、乙两人不在同一个社区的概率；
（3）设随机变量ξ为四名同学中到A社区的人数，求ξ的分布列和Eξ的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】市环保局举办2013年“六五”世界环境日宣传活动，进行现场抽奖．抽奖规则是：盒中装有10张大小相同的精美卡片，卡片上分别印有“环保会徽”或“绿色环保标志”图案．参加者每次从盒中抽取卡片两张，若抽到两张都是“绿色环保标志”卡即可获奖．
（1）活动开始后，一位参加者问：盒中有几张“绿色环保标志”卡？主持人笑说：我只知道若从盒中抽两张都不是“绿色环保标志”卡的概率是
．求抽奖者获奖的概率；
（2）现有甲乙丙丁四人依次抽奖，抽后放回，另一人再抽．用ξ表示获奖的人数．求ξ的分布列及E（ξ），D（ξ）． -
科目： 来源： 题型：
查看答案和解析>>【题目】红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛，甲对A，乙对B，丙对C各一盘，已知甲胜A，乙胜B，丙胜C的概率分别为0.6，0.5，0.5，假设各盘比赛结果相互独立．
（1）求红队至少两名队员获胜的概率；
（2）用ξ表示红队队员获胜的总盘数，求ξ的分布列和数学期望Eξ． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知
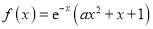.（1）当
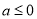时，求证：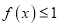 
；（2）当
时，试讨论方程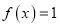
的解的个数. -
科目： 来源： 题型：
查看答案和解析>>【题目】某高校在今年的自主招生考试成绩中随机抽取100名考生的笔试成绩，分为5组制出频率分布直方图如图所示.
（1）求
的值；（2）该校决定在成绩较好的3、4、5组用分层抽样抽取6名学生进行面试，则每组应各抽多少名学生？
（3）在（2）的前提下，已知面试有4位考官，被抽到的6名学生中有两名被指定甲考官面试，其余4名则随机分配给3位考官中的一位对其进行面试，求这4名学生分配到的考官个数
的分布列和期望. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图是函数
的导函数 
的图象，对此图象，有如下结论：
①在区间（-2，1）内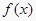
是增函数；
②在区间（1，3）内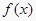 是减函数；
③在
时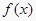， 取得极大值；
④在
时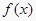， 取得极小值。
其中正确的是 ．
相关试题
