【题目】市环保局举办2013年“六五”世界环境日宣传活动,进行现场抽奖.抽奖规则是:盒中装有10张大小相同的精美卡片,卡片上分别印有“环保会徽”或“绿色环保标志”图案.参加者每次从盒中抽取卡片两张,若抽到两张都是“绿色环保标志”卡即可获奖.
(1)活动开始后,一位参加者问:盒中有几张“绿色环保标志”卡?主持人笑说:我只知道若从盒中抽两张都不是“绿色环保标志”卡的概率是 ![]() .求抽奖者获奖的概率;
.求抽奖者获奖的概率;
(2)现有甲乙丙丁四人依次抽奖,抽后放回,另一人再抽.用ξ表示获奖的人数.求ξ的分布列及E(ξ),D(ξ).
参考答案:
【答案】
(1)解:从盒中任抽两张都不是“绿色环保标志”卡的概率是一个古典概型,
试验发生包含的事件数是C102,设环保会徽卡有n张,则有 ![]() =
= ![]() ,得n=6,所以绿色环保标志”卡有4张,
,得n=6,所以绿色环保标志”卡有4张,
抽奖者获奖的概率为 ![]()
(2)解:ξ可能取的值为0,1,2,3,4,变量ξ服从二项分布,ξ~B(4, ![]() ),根据二项分布的概率公式得到
),根据二项分布的概率公式得到
ξ的分布列为P(ξ=k)= ![]()
ξ | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
E(ξ)= ![]() ,D(ξ)=
,D(ξ)= ![]()
【解析】(1)从盒中任抽两张都不是“绿色环保标志”卡的概率是一个古典概型,试验发生包含的事件数是C102 , 设出环保会徽卡的张数,根据所给的概率的值做出卡片的张数,做出抽奖者获奖的概率.(2)由题意知本题的随机变量满足二项分布,根据二项分布的概率,写出变量的分布列,算出期望.
【考点精析】通过灵活运用离散型随机变量及其分布列,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 在R上可导,其导函数为
在R上可导,其导函数为  且函数
且函数  的图像如图所示,则下列结论一定成立的是( )
的图像如图所示,则下列结论一定成立的是( ) 
A.函数 的极大值是
的极大值是  ,极小值是
,极小值是 
B.函数 的极大值是
的极大值是  ,极小值是
,极小值是 
C.函数 的极大值是
的极大值是  ,极小值是
,极小值是 
D.函数 的极大值是
的极大值是  ,极小值是
,极小值是 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题共12分)已知函数
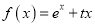 .
.(1)求函数
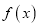 的极值点;
的极值点; (2)若f(x)≥x2+1在(0,2)上恒成立,求实数t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁4名同学被随机地分到A、B、C三个社区参加社会实践,要求每个社区至少有一名同学.
(1)求甲、乙两人都被分到A社区的概率;
(2)求甲、乙两人不在同一个社区的概率;
(3)设随机变量ξ为四名同学中到A社区的人数,求ξ的分布列和Eξ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛,甲对A,乙对B,丙对C各一盘,已知甲胜A,乙胜B,丙胜C的概率分别为0.6,0.5,0.5,假设各盘比赛结果相互独立.
(1)求红队至少两名队员获胜的概率;
(2)用ξ表示红队队员获胜的总盘数,求ξ的分布列和数学期望Eξ. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题共12分)已知函数
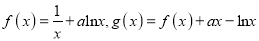
(1)讨论
 的单调性;
的单调性;(2)是否存在常数
 ,使
,使 对任意的
对任意的 和任意的
和任意的 都成立,若存在,求出t的取值范围;若不存在,请说明理由.
都成立,若存在,求出t的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
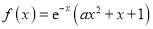 .
.(1)当
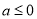 时,求证:
时,求证: 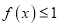 ;
;(2)当
 时,试讨论方程
时,试讨论方程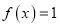 的解的个数.
的解的个数.
相关试题

