【题目】正四棱锥P﹣ABCD,B1为PB的中点,D1为PD的中点,则两个棱锥A﹣B1CD1 , P﹣ABCD的体积之比是( ) 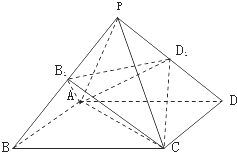
A.1:4
B.3:8
C.1:2
D.2:3
参考答案:
【答案】A
【解析】解答:如图,棱锥A﹣B1CD1 , 的体积可以看成是 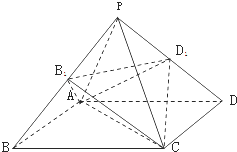
正四棱锥P﹣ABCD的体积减去角上的四个小棱锥的体积得到,
因为B1为PB的中点,D1为PD的中点,
∴棱锥B1﹣ABC,的体积和棱锥D1﹣ACD,的体积都是正四棱锥P﹣ABCD的体积的 ![]() ,
,
棱锥C﹣PB1D1 , 的体积与棱锥A﹣PB1D1的体积之和是正四棱锥P﹣ABCD的体积的 ![]() ,
,
则中间剩下的棱锥A﹣B1CD1的体积
=正四棱锥P﹣ABCD的体积﹣3× ![]() 个正四棱锥P﹣ABCD的体积
个正四棱锥P﹣ABCD的体积
= ![]() 个正四棱锥P﹣ABCD的体积
个正四棱锥P﹣ABCD的体积
则两个棱锥A﹣B1CD1 , P﹣ABCD的体积之比是1:4.
故选A.
分析:如图,棱锥A﹣B1CD1 , 的体积可以看成正四棱锥P﹣ABCD的体积减去角上的四个小棱锥的体积得到,利用底面与高之间的关系得出棱锥B1﹣ABC,的体积和棱锥D1﹣ACD,的体积都是正四棱锥P﹣ABCD的体积的 ![]() ,棱锥C﹣PB1D1 , 的体积与棱锥A﹣PB1D1的体积之和是正四棱锥P﹣ABCD的体积的
,棱锥C﹣PB1D1 , 的体积与棱锥A﹣PB1D1的体积之和是正四棱锥P﹣ABCD的体积的 ![]() ,则中间剩下的棱锥A﹣B1CD1的体积=正四棱锥P﹣ABCD的体积﹣3×
,则中间剩下的棱锥A﹣B1CD1的体积=正四棱锥P﹣ABCD的体积﹣3× ![]() 个正四棱锥P﹣ABCD的体积,最终得到则两个棱锥A﹣B1CD1 , P﹣ABCD的体积之比.
个正四棱锥P﹣ABCD的体积,最终得到则两个棱锥A﹣B1CD1 , P﹣ABCD的体积之比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
: 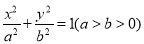 经过点
经过点 ,左右焦点分别为
,左右焦点分别为 、
、 ,圆
,圆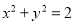 与直线
与直线 相交所得弦长为2.
相交所得弦长为2. (Ⅰ)求椭圆
 的标准方程;
的标准方程;(Ⅱ)设
 是椭圆
是椭圆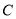 上不在
上不在 轴上的一个动点,
轴上的一个动点,  为坐标原点,过点
为坐标原点,过点 作
作 的平行线交椭圆
的平行线交椭圆 于
于 、
、 两个不同的点,求
两个不同的点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①三点确定一个平面;
②在空间中,过直线外一点只能作一条直线与该直线平行;
③若平面α上有不共线的三点到平面β的距离相等,则α∥β;
④若直线a、b、c满足a⊥b、a⊥c,则b∥c.
其中正确命题的个数是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知空间四边形ABCD,E、H分别是AB、AD的中点,F、G分别是边BC、DC的三等分点(如图),

求证:
(1)对角线AC、BD是异面直线;
(2)直线EF和HG必交于一点,且交点在AC上. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥A﹣BCDE中,底面BCDE为平行四边形,平面ABE⊥平面BCDE,AB=AE,DB=DE,∠BAE=∠BDE=90°
(1)求异面直线AB与DE所成角的大小;
(2)求二面角B﹣AE﹣C的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在
 内的产品为合格品,否则为不合格品,统计结果如表:
内的产品为合格品,否则为不合格品,统计结果如表: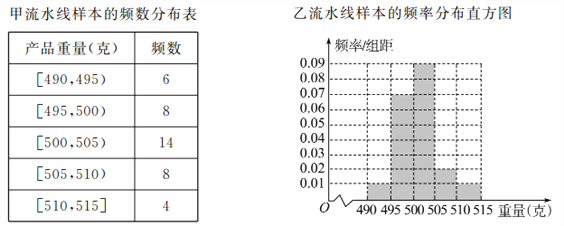
(Ⅰ)求甲流水线样本合格的频率;
(Ⅱ)从乙流水线上重量值落在
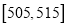 内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】微信已成为人们常用的社交软件,“微信运动”是微信里由腾讯开发的一个类似计步数据库的公众账号.手机用户可以通过关注“微信运动”公众号查看自己每天行走的步数,同时也可以和好友进行运动量的
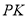 或点赞.现从小明的微信朋友圈内随机选取了40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下表:
或点赞.现从小明的微信朋友圈内随机选取了40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下表:步数
性别
0
 2000
20002001
 5000
50005001
 8000
80008001
 10000
10000>10000
男
1
2
4
7
6
女
0
3
9
6
2
若某人一天的走路步数超过8000步被系统评定为“积极型”,否则被系统评定为“懈怠型”.
(1)利用样本估计总体的思想,试估计小明的所有微信好友中每日走路步数超过10000步的概率;
(2)根据题意完成下面的
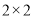 列联表,并据此判断能否有90%的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有90%的把握认为“评定类型”与“性别”有关?积极型
懈怠型
总计
男
女
总计
附:
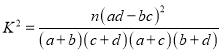
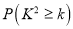
0.10
0.05
0.010
0.005
0.001
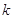
2.706
3.841
6.635
7.879
10.828
相关试题

