【题目】已知空间四边形ABCD,E、H分别是AB、AD的中点,F、G分别是边BC、DC的三等分点(如图), 
求证:
(1)对角线AC、BD是异面直线;
(2)直线EF和HG必交于一点,且交点在AC上.
参考答案:
【答案】
(1)证明:假设对角线AC、BD在同一平面α内,
则A、B、C、D都在平面α内,这与ABCD是空间四边形矛盾,
∴AC、BD是异面直线.
(2)证明:∵E、H分别是AB、AD的中点,∴EH BD.
又F、G分别是BC、DC的三等分点,
∴FG BD.∴EH∥FG,且EH<FG.
∴FE与GH相交.
设交点为O,又O在GH上,GH在平面ADC内,∴O在平面ADC内.
同理,O在平面ABC内.
从而O在平面ADC与平面ABC的交线AC上.
【解析】(1)利用反证法证明对角线AC、BD是共面直线,推出矛盾,从而证明是异面直;(2)说明直线EF和HG必交于一点,然后证明这点在平面ADC内.又在平面ABC内,必在它们的交线AC上.
【考点精析】认真审题,首先需要了解平面的基本性质及推论(如果一条直线上的两点在一个平面内,那么这条直线在此平面内;过不在一条直线上的三点,有且只有一个平面;如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线),还要掌握异面直线的判定(过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.(不在任何一个平面内的两条直线))的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的是(填序号)
①命题“x1 , x2∈M,x1≠x2 , 有[f(x1)﹣f(x2)](x2﹣x1)>0”的否定是“x1 , x2M,x1≠x2 , 有[f(x1)﹣f(x2)](x2﹣x1)≤0”;
②若一个命题的逆命题为真命题,则它的否命题也一定为真命题;
③已知p:x2+2x﹣3>0,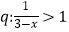 ,若命题(q)∧p为真命题,则x的取值范围是(﹣∞,﹣3)∪(1,2)∪[3,+∞);
,若命题(q)∧p为真命题,则x的取值范围是(﹣∞,﹣3)∪(1,2)∪[3,+∞);
④“x≠3”是“|x|≠3”成立的充分条件. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
: 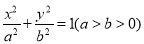 经过点
经过点 ,左右焦点分别为
,左右焦点分别为 、
、 ,圆
,圆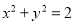 与直线
与直线 相交所得弦长为2.
相交所得弦长为2. (Ⅰ)求椭圆
 的标准方程;
的标准方程;(Ⅱ)设
 是椭圆
是椭圆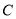 上不在
上不在 轴上的一个动点,
轴上的一个动点,  为坐标原点,过点
为坐标原点,过点 作
作 的平行线交椭圆
的平行线交椭圆 于
于 、
、 两个不同的点,求
两个不同的点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①三点确定一个平面;
②在空间中,过直线外一点只能作一条直线与该直线平行;
③若平面α上有不共线的三点到平面β的距离相等,则α∥β;
④若直线a、b、c满足a⊥b、a⊥c,则b∥c.
其中正确命题的个数是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】正四棱锥P﹣ABCD,B1为PB的中点,D1为PD的中点,则两个棱锥A﹣B1CD1 , P﹣ABCD的体积之比是( )
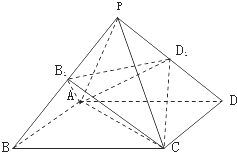
A.1:4
B.3:8
C.1:2
D.2:3 -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥A﹣BCDE中,底面BCDE为平行四边形,平面ABE⊥平面BCDE,AB=AE,DB=DE,∠BAE=∠BDE=90°
(1)求异面直线AB与DE所成角的大小;
(2)求二面角B﹣AE﹣C的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在
 内的产品为合格品,否则为不合格品,统计结果如表:
内的产品为合格品,否则为不合格品,统计结果如表: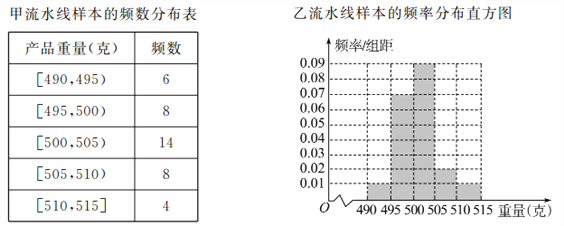
(Ⅰ)求甲流水线样本合格的频率;
(Ⅱ)从乙流水线上重量值落在
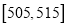 内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
相关试题

