【题目】已知函数f(x)=ax﹣a+1,(a>0且a≠1)恒过定点(2,2).
(1)求实数a;
(2)在(1)的条件下,将函数f(x)的图象向下平移1个单位,再向左平移a个单位后得到函数g(x),设函数g(x)的反函数为h(x),求h(x)的解析式;
(3)对于定义在(1,4]上的函数y=h(x),若在其定义域内,不等式[h(x)+2]2≤h(x2)+h(x)m+6恒成立,求m的取值范围.
参考答案:
【答案】
(1)解:由已知a2﹣a+1=2,∴a=2
(2)解:∵f(x)=2x﹣2+1,
∴g(x)=2x,
∴h(x)=log2x(x>0)
(3)解:要使不等式有意义:则有1<x≤4且1<x2≤4,
∴1<x≤2,
据题有 ![]() 在(1,2]恒成立,
在(1,2]恒成立,
∴设t=log2x(1<x≤2),
∴0<t≤1,
∴(t+2)2≤2t+tm+6在(0,1]时恒成立.
即: ![]() 在[0,1]时恒成立,
在[0,1]时恒成立,
设 ![]() ,t∈(0,1]单调递增,
,t∈(0,1]单调递增,
∴t=1时,有ymax=1,
∴m≥1
【解析】(1)令x=a,则f(a)=2,从而可知f(x)过定点(a,2),再由题设即可求得a值;(2)根据图象平移规则:左加右减,上加下减即可求得g(x)表达式,从而可得h(x)的解析式;(3)令t=log3x,则t∈[0,2],不等式[h(x)+2]2≤h(x2)+m+6 恒成立,可转化为关于t的二次不等式恒成立,进而转化为求函数的最值解决,利用二次函数的性质易求其最值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=
 +lg(﹣x2+4x﹣3)的定义域为M,
+lg(﹣x2+4x﹣3)的定义域为M,
(1)求M;
(2)当x∈M时,求函数f(x)=a2x+2+34x(a<﹣3)的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
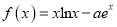 (
(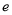 为自然对数的底数)有两个极值点,则实数
为自然对数的底数)有两个极值点,则实数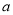 的取值范围是( )
的取值范围是( )A.
 B.
B. 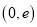 C.
C. 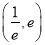 D.
D. 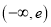
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数f(x)=sin2x的图象向右平移φ(0<φ<
 )个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min=
)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min=  ,则φ=( )
,则φ=( )
A.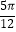
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 sin2x+cos2x﹣m在[0,
sin2x+cos2x﹣m在[0,  ]上有两个零点,则实数m的取值范围是( )
]上有两个零点,则实数m的取值范围是( )
A.(﹣1,2)
B.[1,2)
C.(﹣1,2]
D.[1,2] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x,y满足约束条件
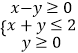 ,若z=ax+y的最大值为4,则a=( )
,若z=ax+y的最大值为4,则a=( )
A.3
B.2
C.﹣2
D.﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中与函数y=x相等的函数是( )
A.y=log22x
B.y=
C.y=2
D.y=( )2
)2
相关试题

