【题目】在10名学生中,男生有x名,现从10名学生中任选6人去参加某项活动:①至少有1名女生;②5名男生,1名女生;③3名男生,3名女生.若要使①为必然事件,②为不可能事件,③为随机事件,则x=( )
A.5B.6C.3或4D.5或6
参考答案:
【答案】C
【解析】
利用必然事件、不可能事件、随机事件的性质求解.
依题意知,10名同学中,男生人数少于5人,但不少于3人,故x=3或4.
故选C
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分,规定满意度不低于98分,则评价该教师为“优秀”,现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶);
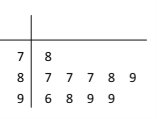
(1)指出这组数据的众数和中位数;
(2)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
(3)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,记
 表示抽到评价该教师为“优秀”的人数,求
表示抽到评价该教师为“优秀”的人数,求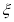 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图.

(1)求分数在
 的频率及全班人数;
的频率及全班人数;(2)求分数在
 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中 间矩形的高;
间矩形的高;(3)若要从分数在
 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在 之间的概率.
之间的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在边长为1的等边三角形
 中,
中, 分别是
分别是 ,
, 上的点,
上的点, ,
, 是
是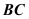 的中点,
的中点,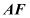 与
与 交于点
交于点 ,
, 沿
沿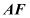 折起,得到如图2所示的三棱锥
折起,得到如图2所示的三棱锥 ,其中
,其中 .
.
(1)求证:平面
 平面
平面
(2)若
 为
为 ,
, 上的中点,
上的中点,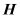 为
为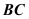 中点,求异面直线
中点,求异面直线 与
与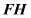 所成角的余弦值
所成角的余弦值 -
科目: 来源: 题型:
查看答案和解析>>【题目】某港口
 要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口
要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口 北偏西
北偏西 且与该港口相距20海里的
且与该港口相距20海里的 处,并以30海里/时的航行速度沿正东方向匀速行驶,假设该小船沿直线方向以
处,并以30海里/时的航行速度沿正东方向匀速行驶,假设该小船沿直线方向以 海里/时的航行速度匀速行驶,经过
海里/时的航行速度匀速行驶,经过 小时与轮船相遇.
小时与轮船相遇.(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/时,试设计航行方案(即确定航行方向与航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过点
 的动直线
的动直线 与抛物线
与抛物线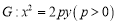 相交于
相交于 、
、 两点.当直线
两点.当直线 的斜率是
的斜率是 时,
时, .
.(1)求抛物线
 的方程;
的方程;(2)设线段
 的中垂线在
的中垂线在 轴上的截距为
轴上的截距为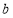 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直角梯形
 所在的平面垂直于平面
所在的平面垂直于平面 ,
,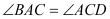
 .
.
(1)在直线
 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ?请证明你的结论.
?请证明你的结论.(2)求平面
 与平面
与平面 所成的锐二面角
所成的锐二面角 的余弦值.
的余弦值.
相关试题

