【题目】已知过点![]() 的动直线
的动直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点.当直线
两点.当直线![]() 的斜率是
的斜率是![]() 时,
时,![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设线段![]() 的中垂线在
的中垂线在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题分析:(1)设![]() ,
,![]() ,当直线
,当直线![]() 的斜率是
的斜率是![]() 时,
时,![]() 的方程为
的方程为![]() ,即
,即![]()
由![]() ,得
,得![]() ,可得
,可得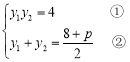 ;又
;又![]() ,∴
,∴![]() ③
③
由①、②、③及![]() 得由此即可求出结果;(2)设
得由此即可求出结果;(2)设![]() ,
,![]() 中点坐标为
中点坐标为![]()
由![]() ,得
,得![]() ④,可得
④,可得![]() ,
,![]() ,由此可得线段
,由此可得线段![]() 的中垂线方程为
的中垂线方程为![]() ,进而求出线段
,进而求出线段![]() 的中垂线在
的中垂线在![]() 轴上的截距为:
轴上的截距为:![]() ,由此即可求出结果.
,由此即可求出结果.
试题解析:解:(1)设![]() ,
,![]() ,当直线
,当直线![]() 的斜率是
的斜率是![]() 时,
时,![]() 的方程为
的方程为![]() ,即
,即![]()
由![]() ,得
,得![]() ,
,
∴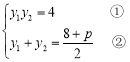
又∵![]() ,∴
,∴![]() ③
③
由①、②、③及![]() 得:
得:![]() ,
,![]() ,
,![]() ,则抛物线
,则抛物线![]() 的方程为:
的方程为:![]() .
.
(2)设![]() ,
,![]() 中点坐标为
中点坐标为![]()
由![]() ,得
,得![]() ④
④
∴![]() ,
,![]() ,
,
∴线段![]() 的中垂线方程为
的中垂线方程为![]() ,
,
∴线段![]() 的中垂线在
的中垂线在![]() 轴上的截距为:
轴上的截距为:
![]() ,
,
对于方程④,由![]() 得:
得:![]() 或
或![]() .
.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在边长为1的等边三角形
 中,
中, 分别是
分别是 ,
, 上的点,
上的点, ,
, 是
是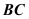 的中点,
的中点,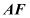 与
与 交于点
交于点 ,
, 沿
沿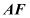 折起,得到如图2所示的三棱锥
折起,得到如图2所示的三棱锥 ,其中
,其中 .
.
(1)求证:平面
 平面
平面
(2)若
 为
为 ,
, 上的中点,
上的中点,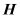 为
为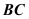 中点,求异面直线
中点,求异面直线 与
与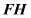 所成角的余弦值
所成角的余弦值 -
科目: 来源: 题型:
查看答案和解析>>【题目】在10名学生中,男生有x名,现从10名学生中任选6人去参加某项活动:①至少有1名女生;②5名男生,1名女生;③3名男生,3名女生.若要使①为必然事件,②为不可能事件,③为随机事件,则x=( )
A.5B.6C.3或4D.5或6
-
科目: 来源: 题型:
查看答案和解析>>【题目】某港口
 要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口
要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口 北偏西
北偏西 且与该港口相距20海里的
且与该港口相距20海里的 处,并以30海里/时的航行速度沿正东方向匀速行驶,假设该小船沿直线方向以
处,并以30海里/时的航行速度沿正东方向匀速行驶,假设该小船沿直线方向以 海里/时的航行速度匀速行驶,经过
海里/时的航行速度匀速行驶,经过 小时与轮船相遇.
小时与轮船相遇.(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/时,试设计航行方案(即确定航行方向与航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直角梯形
 所在的平面垂直于平面
所在的平面垂直于平面 ,
,
 .
.
(1)在直线
 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ?请证明你的结论.
?请证明你的结论.(2)求平面
 与平面
与平面 所成的锐二面角
所成的锐二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能来回16次,如果每次拖7节车厢,则每日能来回10次.
(1)若每日来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数解析式:
(2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在单调递增数列
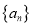 中,
中, 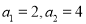 ,且
,且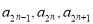 成等差数列,
成等差数列, 成等比数列,
成等比数列,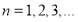 .
. (1)①求证:数列
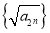 为等差数列;
为等差数列;②求数列
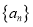 通项公式;
通项公式;(2)设数列
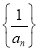 的前
的前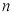 项和为
项和为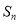 ,证明:
,证明: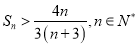 .
.
相关试题

