【题目】设二次函数f(x)满足f(2+x)=f(2-x),对于x∈R恒成立,且f(x)=0的两个实数根的平方和为10,f(x)的图象过点(0,3),求f(x)的解析式.
参考答案:
【答案】![]() .
.
【解析】试题分析: 二次函数f(x)满足f(2+x)=f(2-x)可知, 图象关于直线x=2对称, 设f(x)=a(x-2)2+k(a≠0),图象过点(0,3),可得k=3-4a,再用f(x)=0的两个实数根的平方和为10,写出韦达定理代入求出a值,进而得出f(x)的解析式.
试题解析:
∵f(2+x)=f(2-x),∴f(x)的图象关于直线x=2对称.于是,设f(x)=a(x-2)2+k(a≠0), 则由f(0)=3,可得k=3-4a,∴f(x)=a(x-2)2+3-4a=ax2-4ax+3.∵ax2-4ax+3=0的两实数根的平方和为10,∴10=x+x=(x1+x2)2-2x1x2=16-![]() ,∴a=1,∴
,∴a=1,∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从某企业生产的产品中抽取1000件测量这些产品的一项质量指标值,由测量结果得到频率分布直方图如图所示.
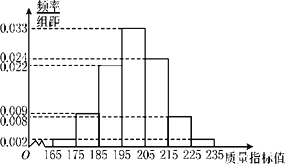
(Ⅰ)求这1000件产品质量指标值的样本平均数
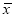 和样本方差s2(同一组数据用该区间的中点值作代表).
和样本方差s2(同一组数据用该区间的中点值作代表).(Ⅱ)由频率分布直方图可以认为这种产品的质量指标值Z服从正态分布N(μ,δ2),其中μ近似为样本平均数
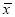 ,δ2近似为样本方差s2.
,δ2近似为样本方差s2. 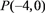 利用该正态分布,求P(175.6<Z<224.4);
利用该正态分布,求P(175.6<Z<224.4);②某用户从该企业购买了100件这种产品,估计其中质量指标值位于区间(175.6,224.4)的产品件数.(精确到个位)
附:
 ≈12.2,若Z~N(μ,δ2),则P(μ-δ<Z<μ+δ)=0.6826,
≈12.2,若Z~N(μ,δ2),则P(μ-δ<Z<μ+δ)=0.6826,P(μ-2δ<Z<μ+2δ)=0.9544
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
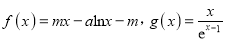 ,其中
,其中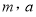 均为实数,
均为实数, 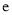 为自然对数的底数.
为自然对数的底数.(I)求函数
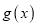 的极值;
的极值;(II)设
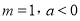 ,若对任意的
,若对任意的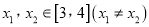 ,
,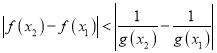 恒成立,求实数
恒成立,求实数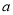 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为调查大学生这个微信用户群体中每人拥有微信群的数量,现从武汉市大学生中随机抽取100位同学进行了抽样调查,结果如下:
微信群数量
频数
频率
0至5个
0
0
6至10个
30
0.3
11至15个
30
0.3
16至20个
a
c
20个以上
5
b
合计
100
1
(Ⅰ)求a,b,c的值;
(Ⅱ)以这100个人的样本数据估计武汉市的总体数据且以频率估计概率,若从全市大学生(数量很大)中随机抽取3人,记X表示抽到的是微信群个数超过15个的人数,求X的分布列和数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设p:实数x满足
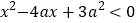 ,其中
,其中 ,命题
,命题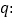 实数
实数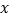 满足
满足|x-3|≤1 .
(1)若
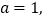 且
且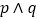 为真,求实数
为真,求实数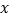 的取值范围;
的取值范围;(2)若
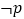 是
是
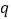 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x+4)+f(x-1)=x2-2x,其中f(x)是二次函数,求函数f(x)的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
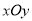 中,曲线
中,曲线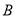 是过点
是过点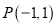 ,倾斜角为
,倾斜角为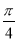 的直线,以直角坐标系
的直线,以直角坐标系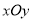 的原点为极点,
的原点为极点, 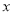 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线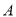 的极坐标方程是
的极坐标方程是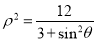 .
.(1)求曲线
 的普通方程和曲线
的普通方程和曲线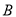 的一个参数方程;
的一个参数方程;(2)曲线
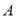 与曲线
与曲线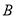 相交于
相交于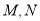 两点,求
两点,求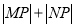 的值.
的值.
相关试题

