【题目】为调查大学生这个微信用户群体中每人拥有微信群的数量,现从武汉市大学生中随机抽取100位同学进行了抽样调查,结果如下:
微信群数量 | 频数 | 频率 |
0至5个 | 0 | 0 |
6至10个 | 30 | 0.3 |
11至15个 | 30 | 0.3 |
16至20个 | a | c |
20个以上 | 5 | b |
合计 | 100 | 1 |
(Ⅰ)求a,b,c的值;
(Ⅱ)以这100个人的样本数据估计武汉市的总体数据且以频率估计概率,若从全市大学生(数量很大)中随机抽取3人,记X表示抽到的是微信群个数超过15个的人数,求X的分布列和数学期望.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)由频率分布列的性质及频率=频数/总数,,能求出![]() 的值.
的值.
(Ⅱ)依题意可知,微信群个数超过15个的概率为![]() ,根据二项分布求解即可.
,根据二项分布求解即可.
试题解析:
(Ⅰ)由已知得:0+30+30+a+5=100, 解得a=35,
![]() .
.
(Ⅱ)依题意可知,微信群个数超过15个的概率为![]() .
.
X的所有可能取值0,1,2,3.
则![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
其分布列如下:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以,![]() .
. ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产A,B两种产品,根据市场调查与市场预测,知A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2.(注:所示图中的横坐标表示投资金额,单位:万元)

图1 图2
(1)分别将A,B两种产品的利润表示为投资的函数关系式;
(2)该企业已筹集10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元资金,才能使企业获得最大利润,最大利润为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】从某企业生产的产品中抽取1000件测量这些产品的一项质量指标值,由测量结果得到频率分布直方图如图所示.
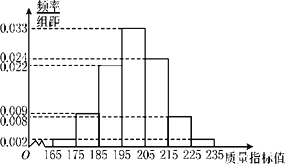
(Ⅰ)求这1000件产品质量指标值的样本平均数
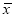 和样本方差s2(同一组数据用该区间的中点值作代表).
和样本方差s2(同一组数据用该区间的中点值作代表).(Ⅱ)由频率分布直方图可以认为这种产品的质量指标值Z服从正态分布N(μ,δ2),其中μ近似为样本平均数
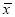 ,δ2近似为样本方差s2.
,δ2近似为样本方差s2. 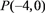 利用该正态分布,求P(175.6<Z<224.4);
利用该正态分布,求P(175.6<Z<224.4);②某用户从该企业购买了100件这种产品,估计其中质量指标值位于区间(175.6,224.4)的产品件数.(精确到个位)
附:
 ≈12.2,若Z~N(μ,δ2),则P(μ-δ<Z<μ+δ)=0.6826,
≈12.2,若Z~N(μ,δ2),则P(μ-δ<Z<μ+δ)=0.6826,P(μ-2δ<Z<μ+2δ)=0.9544
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
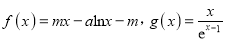 ,其中
,其中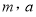 均为实数,
均为实数, 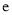 为自然对数的底数.
为自然对数的底数.(I)求函数
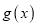 的极值;
的极值;(II)设
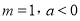 ,若对任意的
,若对任意的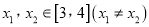 ,
,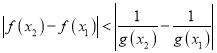 恒成立,求实数
恒成立,求实数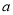 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设二次函数f(x)满足f(2+x)=f(2-x),对于x∈R恒成立,且f(x)=0的两个实数根的平方和为10,f(x)的图象过点(0,3),求f(x)的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设p:实数x满足
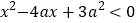 ,其中
,其中 ,命题
,命题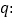 实数
实数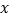 满足
满足|x-3|≤1 .
(1)若
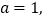 且
且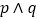 为真,求实数
为真,求实数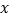 的取值范围;
的取值范围;(2)若
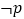 是
是
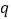 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x+4)+f(x-1)=x2-2x,其中f(x)是二次函数,求函数f(x)的解析式.
相关试题

