【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时, ![]() ;
;
(1)求函数![]() 在
在![]() 上的解析式并画出函数
上的解析式并画出函数![]() 的图象(不要求列表描点,只要求画出草图)
的图象(不要求列表描点,只要求画出草图)
(2)(ⅰ)写出函数![]() 的单调递增区间;
的单调递增区间;
(ⅱ)若方程![]() 在
在![]() 上有两个不同的实数根,求实数
上有两个不同的实数根,求实数![]() 的取值范围。
的取值范围。
参考答案:
【答案】(1)![]() (2)(ⅰ)
(2)(ⅰ)![]() 和
和![]() (ⅱ)
(ⅱ)![]()
【解析】试题分析:(1)设![]() 则
则![]() , 有
, 有![]() ,结合
,结合![]() 为奇函数,所以
为奇函数,所以![]() ,可得
,可得![]() 的解析式
的解析式
(2)(ⅰ)由图象可得函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]()
(ⅱ)方程![]() 在
在![]() 上有两个不同的实数根,转化为函数
上有两个不同的实数根,转化为函数![]() 与
与![]() 在
在![]() 上有两个不同的交点,由图象得
上有两个不同的交点,由图象得![]() ,所以
,所以![]()
试题解析:(1)设![]() 则
则![]()
所以![]()
又因为![]() 为奇函数,所以
为奇函数,所以![]()
所以![]() 即
即![]()
![]()
所以![]()
图象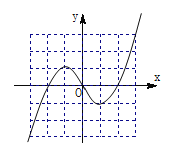
(2)(ⅰ)由图象得函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]()
(ⅱ)方程![]() 在
在![]() 上有两个不同的实数根,
上有两个不同的实数根,
所以函数![]() 与
与![]() 在
在![]() 上有两个不同的交点,
上有两个不同的交点,
由图象得![]() ,所以
,所以![]()
所以实数![]() 的取值范围为
的取值范围为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos 2A-3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5
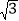 ,b=5,求sin Bsin C的值.
,b=5,求sin Bsin C的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
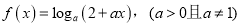
(1)设
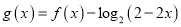 ,当
,当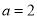 时,求函数
时,求函数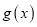 的定义域,判断并证明函数
的定义域,判断并证明函数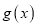 的奇偶性;
的奇偶性;(2)是否存在实数
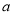 ,使得函数
,使得函数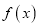 在
在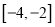 递减,并且最小值为1,若存在,求出
递减,并且最小值为1,若存在,求出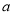 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
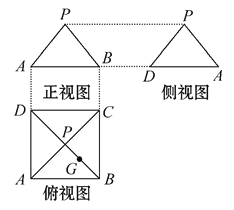
(1)根据三视图,画出该几何体的直观图.
(2)在直观图中,①证明:PD∥平面AGC;
②证明:平面PBD⊥平面AGC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
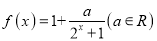 .
.(1)当
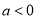 时,判断并证明函数
时,判断并证明函数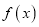 在
在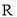 上单调性。
上单调性。(2)当
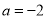 时,若关于
时,若关于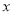 的方程
的方程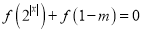 在
在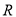 上有解,求实数
上有解,求实数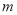 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥PABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________.(写出所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】从某市主办的科技知识竞赛的学生成绩中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组,第一组
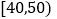 ;第二组
;第二组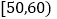 ;…;第六组
;…;第六组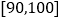 ,并据此绘制了如图所示的频率分布直方图.
,并据此绘制了如图所示的频率分布直方图.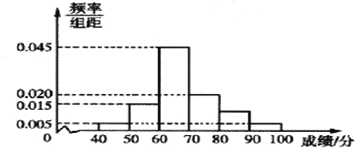
(1)求成绩在区间
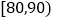 内的学生人数;
内的学生人数;(2)从成绩大于等于80分的学生中随机选取2名,求至少有1名学生的成绩在区间
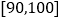 内的概率.
内的概率.
相关试题

