【题目】已知![]() ,函数
,函数![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程.
处的切线方程.
(Ⅱ)求![]() 在区间
在区间![]() 上的最小值.
上的最小值.
参考答案:
【答案】(![]() )
)![]() .(
.(![]() )见解析.
)见解析.
【解析】试题分析:(1)求出f'(x),得切线的斜率![]() ,又曲线的切点为(2,f(2)),由点斜式可写出切线方程;
,又曲线的切点为(2,f(2)),由点斜式可写出切线方程;
(2)借助于导数,将函数![]() 的最值问题转化为导函数进行研究.分
的最值问题转化为导函数进行研究.分![]() ,
, ![]() ,
, ![]() 三种情况讨论函数的最值情况.
三种情况讨论函数的最值情况.
试题解析:(![]() )当
)当![]() 时,
时, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,即曲线
,即曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() .
.
又∵![]() ,
,
∴曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() .
.
(![]() )∵
)∵![]() ,∴
,∴![]() .
.
令![]() ,得
,得![]() .
.
①若![]() ,则
,则![]() ,
, ![]() 在区间
在区间![]() 上单调递增,此时函数
上单调递增,此时函数![]() 无最小值.
无最小值.
②若![]() ,当
,当![]() 时,
时, ![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
当![]() 时,
时, ![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以当![]() 时,函数
时,函数![]() 取得最小值
取得最小值![]() .
.
③当![]() ,则当
,则当![]() 时,
时, ![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以当![]() 时,函数
时,函数![]() 取得最小值
取得最小值![]() .
.
综上所述,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上无最小值.
上无最小值.
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
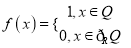 ,则(ⅰ)
,则(ⅰ)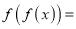 ____________.
____________.(ⅱ)给出下列三个命题:①函数
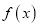 是偶函数;②存在
是偶函数;②存在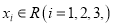 ,使得以点
,使得以点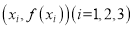 为顶点的三角形是等腰三角形;③存在
为顶点的三角形是等腰三角形;③存在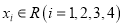 ,使得以点
,使得以点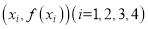 为顶点的四边形为菱形.
为顶点的四边形为菱形.其中,所有真命题的序号是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举行一次“环保知识竞赛”,全校学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为
 分)作为样本进行统计,请根据下面尚未完成并有局部污损的样本的频率分布表和频率分布直方图(如图所示)解决下列问题:
分)作为样本进行统计,请根据下面尚未完成并有局部污损的样本的频率分布表和频率分布直方图(如图所示)解决下列问题:(Ⅰ)写出
 ,
,  ,
,  ,
,  的值.
的值.(Ⅱ)在选取的样本中,从竞赛成绩是
 分以上(含
分以上(含 分)的同学中随机抽取
分)的同学中随机抽取 名同学到广场参加环保知识的志愿宣传活动,求所抽取的
名同学到广场参加环保知识的志愿宣传活动,求所抽取的 名同学来自同一组的概率.
名同学来自同一组的概率.(Ⅲ)在(Ⅱ)的条件下,设
 表示所抽取的
表示所抽取的 名同学中来自第
名同学中来自第 组的人数,求
组的人数,求 的分布列及其数学期望.
的分布列及其数学期望.组别
分组
频数
频率
第
 组
组


第
 组
组


第
 组
组


第
 组
组


第
 组
组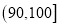


合计



-
科目: 来源: 题型:
查看答案和解析>>【题目】己知四棱锥
 中,
中,  平面
平面 ,底面
,底面 是菱形,且
是菱形,且 .
.  ,
,  、
、 的中点分别为
的中点分别为 ,
,  .
.(Ⅰ)求证
 .
.(Ⅱ)求二面角
 的余弦值.
的余弦值.(Ⅲ)在线段
 上是否存在一点
上是否存在一点 ,使得
,使得 平行于平面
平行于平面 ?若存在,指出
?若存在,指出 在
在 上的位置并给予证明,若不存在,请说明理由.
上的位置并给予证明,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
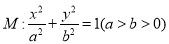 过点
过点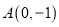 ,且离心率
,且离心率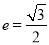 .
.(Ⅰ)求椭圆
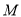 的方程.
的方程.(Ⅱ)若椭圆
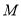 上存在点
上存在点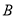 、
、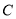 关于直线
关于直线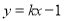 对称,求
对称,求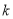 的所有取值构成的集合
的所有取值构成的集合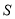 ,并证明对于
,并证明对于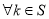 ,
, 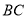 的中点恒在一条定直线上.
的中点恒在一条定直线上. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为
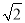 的正方形
的正方形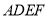 与梯形
与梯形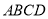 所在的平面互相垂直,其中
所在的平面互相垂直,其中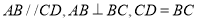 ,
, 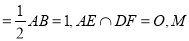 为
为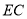 的中点.
的中点.(Ⅰ)证明:
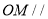 平面
平面 ;
;(Ⅱ)求
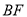 与平面
与平面 所成角的余弦值.
所成角的余弦值.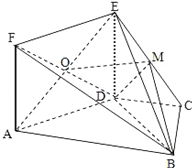
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年12月10日,我国科学家屠呦呦教授由于在发现青蒿素和治疗疟疾的疗法上的贡献获得诺贝尔医学奖,以青蒿素类药物为主的联合疗法已经成为世界卫生组织推荐的抗疟疾标准疗法,目前,国内青蒿人工种植发展迅速,调查表明,人工种植的青蒿的长势与海拨高度、土壤酸碱度、空气湿度的指标有极强的相关性,现将这三项的指标分别记为
 ,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标
,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标 的值评定人工种植的青蒿的长势等级,若
的值评定人工种植的青蒿的长势等级,若 ,则长势为一级;若
,则长势为一级;若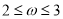 ,则长势为二极;若
,则长势为二极;若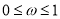 ,则长势为三级,为了了解目前人工种植的青蒿的长势情况,研究人员随机抽取了10块青蒿人工种植地,得到如下结果:
,则长势为三级,为了了解目前人工种植的青蒿的长势情况,研究人员随机抽取了10块青蒿人工种植地,得到如下结果:种植地编号
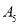
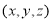
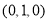
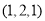
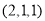

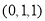
种植地编号
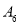
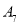
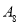
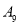
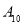
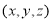




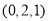
(1)若该地有青蒿人工种植地180个,试估计该地中长势等级为三级的个数;
(2)从长势等级为一级的青蒿人工种植地中随机抽取两个,求这两个人工种植地的综合指标
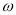 均为4个概率.
均为4个概率.
相关试题

