【题目】如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的表面积(其中∠BAC=30°)及其体积. 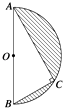
参考答案:
【答案】解:如图所示,过C作CO1⊥AB于O1 , 在半圆中可得∠BCA=90°,∠BAC=30°,AB=2R, ∴AC= ![]() R,BC=R,CO1=
R,BC=R,CO1= ![]() R,
R,
∴S球=4πR2 , ![]() =π×
=π× ![]() R×
R× ![]() R=
R= ![]() πR2 ,
πR2 , ![]() =π×
=π× ![]() R×R=
R×R= ![]() πR2 ,
πR2 ,
∴S几何体表=S球+ ![]() +
+ ![]() =
= ![]() πR2 ,
πR2 ,
∴旋转所得到的几何体的表面积为 ![]() πR2 .
πR2 .
又V球= ![]() πR3 ,
πR3 , ![]() =
= ![]() AO1πCO12=
AO1πCO12= ![]() πR2AO1
πR2AO1![]() =
= ![]() BO1πCO12=
BO1πCO12= ![]() BO1πR2
BO1πR2
∴V几何体=V球﹣( ![]() +
+ ![]() )=
)= ![]() πR3 .
πR3 . 
【解析】求出AC= ![]() R,BC=R,CO1=
R,BC=R,CO1= ![]() R,再求出几何体的表面积;要求旋转后阴影部分的体积即是球的体积减去两个圆锥的体积,根据圆锥的体积公式和球的体积公式进行计算.
R,再求出几何体的表面积;要求旋转后阴影部分的体积即是球的体积减去两个圆锥的体积,根据圆锥的体积公式和球的体积公式进行计算.
【考点精析】通过灵活运用旋转体(圆柱、圆锥、圆台),掌握常见的旋转体有:圆柱、圆锥、圆台、球即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的首项a1=a,Sn是数列{an}的前n项和,且满足:Sn2=3n2an+Sn﹣12 , an≠0,n≥2,n∈N* .
(1)若数列{an}是等差数列,求a的值;
(2)确定a的取值集合M,使a∈M时,数列{an}是递增数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)证明:当
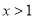 时,
时, 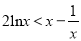 ;
;(2)若不等式
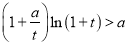 对任意的正实数
对任意的正实数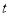 恒成立,求正实数
恒成立,求正实数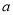 的取值范围;
的取值范围;(3)求证:
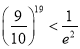 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满a1=a,a2=b,3an+2﹣5an+1+2an=0(n≥0,n∈N),求数列{an}的通项公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<
 )在某一个周期内的图象时,列表并填入的部分数据如表:
)在某一个周期内的图象时,列表并填入的部分数据如表: x

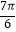
ωx+φ
0

π
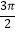
2π
Asin(ωx+φ)
0
2
0
﹣2
(1)请将上表数据补全,并直接写出函数f(x)的解析式;
(2)当x∈[0, ]时,求函数f(x)的值域.
]时,求函数f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知单位圆O上的两点A,B及单位圆所在平面上的一点P,满足
 =m
=m  +
+  (m为常数).
(m为常数). 
(1)如图,若四边形OABP为平行四边形,求m的值;
(2)若m=2,求| |的取值范围.
|的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 =(2cos2x,
=(2cos2x,  ),
),  =(1,sin2x),函数f(x)=
=(1,sin2x),函数f(x)= 
 ﹣1.
﹣1.
(1)当x= 时,求|a﹣b|的值;
时,求|a﹣b|的值;
(2)求函数f(x)的最小正周期以及单调递增区间;
(3)求方程f(x)=k,(0<k<2),在[﹣ ,
,  ]内的所有实数根之和.
]内的所有实数根之和.
相关试题

