【题目】已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2 , a4的等差中项.
(1)求数列{an}的通项公式
(2)若bn=anlog ![]() an , Sn=b1+b2+b3+…+bn , 对任意正整数n,Sn+(n+m)an+1<0恒成立,试求m的取值范围.
an , Sn=b1+b2+b3+…+bn , 对任意正整数n,Sn+(n+m)an+1<0恒成立,试求m的取值范围.
参考答案:
【答案】
(1)解:设等比数列{an}的首项为a1,公比为q.
依题意,
有2(a3+2)=a2+a4,
代入a2+a3+a4=28,
得a3=8.
∴a2+a4=20.
∴ ![]()
解之得 ![]() ,或
,或 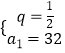
又{an}单调递增,
∴q=2,a1=2,∴an=2n,
(2)解:bn=2nlog ![]() 2n=﹣n2n,
2n=﹣n2n,
∴﹣Sn=1×2+2×22+3×23++n×2n①
﹣2Sn=1×22+2×23++(n﹣1)2n+n2n+1②
①﹣②得,Sn=2+22+23++2n﹣n2n+1
= ![]() ﹣n2n+1
﹣n2n+1
=2n+1﹣2﹣n2n+1
由Sn+(n+m)an+1<0,
即2n+1﹣2﹣n2n+1+n2n+1+m2n+1<0对任意正整数n恒成立,
∴m2n+1<2﹣2n+1.
对任意正整数n,
m< ![]() ﹣1恒成立.
﹣1恒成立.
∵ ![]() ﹣1>﹣1,∴m≤﹣1.
﹣1>﹣1,∴m≤﹣1.
即m的取值范围是(﹣∞,﹣1].
【解析】(1)设等比数列{an}的首项为a1 , 公比为q,根据2(a3+2)=a2+a4 , 可求得a3 . 进而求得a2+a4=20.两式联立方程即可求得a1和q的值,最后根据等比数列的通项公式求得an . (2)把(1)中的an代入bn , 再利用错位相减法求得Sn , 再由Sn+(n+m)an+1<0恒成立进而求得m的范围.
【考点精析】解答此题的关键在于理解等比数列的基本性质的相关知识,掌握{an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c分别是△ABC的角A,B,C所对的边,且c=2,C=
 .
.
(1)若△ABC的面积等于 ,求a,b;
,求a,b;
(2)若sinC+sin(B﹣A)=2sin2A,求A的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】交警随机抽取了途径某服务站的40辆小型轿车在经过某区间路段的车速(单位:
 ),现将其分成六组为
),现将其分成六组为 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.(1)某小型轿车途经该路段,其速度在
 以上的概率是多少?
以上的概率是多少?(2)若对车速在
 两组内进一步抽测两辆小型轿车,求至少有一辆小型轿车速度在
两组内进一步抽测两辆小型轿车,求至少有一辆小型轿车速度在 内的概率.
内的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
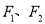 是双曲线
是双曲线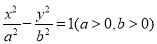 的左右焦点,以
的左右焦点,以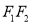 为直径的圆与双曲线的一条渐近线交于点
为直径的圆与双曲线的一条渐近线交于点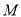 ,与双曲线交于点
,与双曲线交于点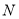 ,且
,且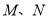 均在第一象限,当直线
均在第一象限,当直线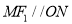 时,双曲线的离心率为
时,双曲线的离心率为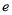 ,若函数
,若函数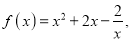 ,则
,则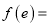 ()
()A. 1 B.
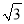 C. 2 D.
C. 2 D. 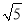
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
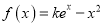 (其中
(其中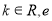 是自然对数的底数)
是自然对数的底数)(1)若
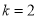 ,当
,当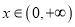 时,试比较
时,试比较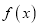 与2的大小;
与2的大小;(2)若函数
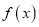 有两个极值点
有两个极值点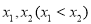 ,求
,求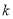 的取值范围,并证明:
的取值范围,并证明: 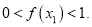
-
科目: 来源: 题型:
查看答案和解析>>【题目】设等差数列{an}满足
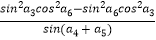 =1,公差d∈(﹣1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,求该数列首项a1的取值范围( )
=1,公差d∈(﹣1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,求该数列首项a1的取值范围( )
A.(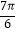 ,
, 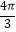 )
)
B.[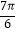 ,
, 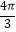 ]
]
C.(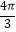 ,
, 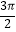 )
)
D.[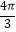 ,
, 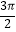 ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
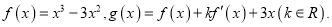
(1)讨论
 的单调性;
的单调性;(2)若直线
 与曲线
与曲线 都只有两个交点,证明:这四个交点可以构成一个平行四边形,并计算该平行四边形的面积.
都只有两个交点,证明:这四个交点可以构成一个平行四边形,并计算该平行四边形的面积.
相关试题

