【题目】已知函数f(x)=|x+2|﹣2|x﹣1|.
(1)解不等式f(x)≥﹣2;
(2)对任意x∈R,都有f(x)≤x﹣a成立,求实数a的取值范围.
参考答案:
【答案】
(1)解:f(x)= 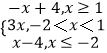 .
.
∵f(x)≥﹣2,
∴ ![]() 或
或 ![]() 或
或 ![]() ,
,
解得1≤x≤6或﹣ ![]() ≤x<1.
≤x<1.
∴不等式f(x)≥﹣2的解为集为{x|﹣ ![]() ≤x≤6}.
≤x≤6}.
(2)解:当x≥1时,﹣x+4≤x﹣a,即a≤2x﹣4恒成立,∴a≤﹣2;
当﹣2<x<1时,3x≤x﹣a,即a≤﹣2x恒成立,∴a≤﹣2;
当x≤﹣2时,x﹣4≤x﹣a,即a≤4恒成立.
∵任意x∈R,都有f(x)≤x﹣a成立,
∴a≤﹣2
【解析】(1)去绝对值符号得出f(x)的分段解析式,再各段上解不等式即可;(2)对x的范围进行讨论,分离参数得出a在各段上的最小值,即可得出a的范围.
【考点精析】解答此题的关键在于理解不等式的证明的相关知识,掌握不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各函数在其定义域中,既是奇函数,又是增函数的是( )
A.y=x+1
B.y=﹣x3
C.y=﹣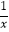
D.y=x|x| -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣2ax﹣3
(1)若函数在f(x)的单调递减区间(﹣∞,2],求函数f(x)在区间[3,5]上的最大值.
(2)若函数在f(x)在单区间(﹣∞,2]上是单调递减,求函数f(1)的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在体积为72的直三棱柱ABC﹣A1B1C1中,AB=3,AC=4,AA1=12.
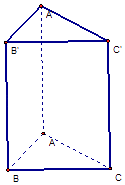
(1)求角∠BAC的大小;
(2)若该三棱柱的六个顶点都在球O的球面上,求球O的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列对应值如下表:
x

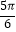
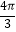

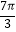
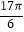
y
﹣1
1
3
1
﹣1
1
3
(1)根据表格提供的数据求函数f(x)的一个解析式.
(2)根据(1)的结果,若函数y=f(kx)(k>0)周期为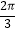 ,当
,当 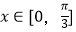 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
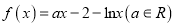
(1)若
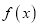 在点
在点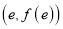 处的切线斜率为
处的切线斜率为 ,求
,求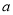 的值;
的值;(2)求函数
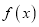 的单调区间;
的单调区间;(3)若
 ,求证:在
,求证:在 时,
时,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=a﹣
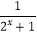 .
.
(1)求证:函数f(x)在R上为增函数;
(2)当函数f(x)为奇函数时,求函数f(x)在[﹣1,2]上的值域.
相关试题

