【题目】设函数![]()
(1)若![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,求
,求![]() 的值;
的值;
(2)求函数![]() 的单调区间;
的单调区间;
(3)若![]() ,求证:在
,求证:在![]() 时,
时, ![]() .
.
参考答案:
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]() .单调增区间为
.单调增区间为![]() ;
;
当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)先求出![]() ,通过
,通过![]() 在点
在点![]() 处的切线斜率,可得
处的切线斜率,可得![]() ,解得
,解得![]() ;(2)由(1)知:
;(2)由(1)知: ![]() ,结合导数分①
,结合导数分①![]() 、②
、②![]() 两种情况讨论分别令
两种情况讨论分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;;(3)通过变形,只需证明
的减区间;;(3)通过变形,只需证明![]() 即可,利用
即可,利用![]() ,根据指数函数及幂函数的性质、函数的单调性及零点判定定理即得到结论.
,根据指数函数及幂函数的性质、函数的单调性及零点判定定理即得到结论.
试题解析:(1)若![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,
,
![]() ,
,
得![]() .
.
(2)由![]()
当![]() 时,令
时,令![]() 解得:
解得: ![]()
当![]() 变化时,
变化时, ![]() 随
随![]() 变化情况如表:
变化情况如表:
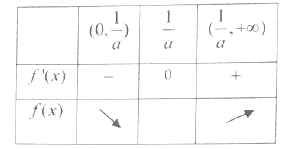
由表可知: ![]() 在
在![]() 上是单调减函数,在
上是单调减函数,在![]() 上是单调增函数
上是单调增函数
当![]() 时,
时, ![]() ,
, ![]() 的单调减区间为
的单调减区间为![]()
所以,当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]() .单调增区间为
.单调增区间为![]()
当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]()
(3)当![]() 时,要证
时,要证![]() ,即证
,即证![]()
令![]() ,只需证
,只需证![]()
∵![]()
由指数函数及幕函数的性质知: ![]() 在
在![]() 上是增函数
上是增函数
∵![]() ,∴
,∴![]() 在
在![]() 内存在唯一的零点,
内存在唯一的零点,
也即![]() 在
在![]() 上有唯一零点
上有唯一零点
设![]() 的零点为
的零点为![]() ,则
,则![]() ,即
,即![]() ,
,
由![]() 的单调性知:
的单调性知:
当![]() 时,
时, ![]() ,
, ![]() 为减函数
为减函数
当![]() 时,
时, ![]() ,
, ![]() 为增函数,
为增函数,
所以当![]() 时.
时.
![]()
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在体积为72的直三棱柱ABC﹣A1B1C1中,AB=3,AC=4,AA1=12.
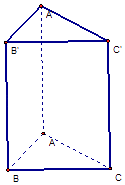
(1)求角∠BAC的大小;
(2)若该三棱柱的六个顶点都在球O的球面上,求球O的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x+2|﹣2|x﹣1|.
(1)解不等式f(x)≥﹣2;
(2)对任意x∈R,都有f(x)≤x﹣a成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列对应值如下表:
x
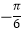

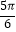
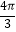

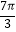
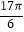
y
﹣1
1
3
1
﹣1
1
3
(1)根据表格提供的数据求函数f(x)的一个解析式.
(2)根据(1)的结果,若函数y=f(kx)(k>0)周期为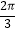 ,当
,当 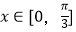 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=a﹣
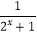 .
.
(1)求证:函数f(x)在R上为增函数;
(2)当函数f(x)为奇函数时,求函数f(x)在[﹣1,2]上的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
 的前n项和为
的前n项和为 ,
,  ,
,  ,数列
,数列 满足:
满足:  ,
,  ,
,  ,数列
,数列 的前n项和为
的前n项和为
(1)求数列
 的通项公式及前n项和;
的通项公式及前n项和;(2)求数列
 的通项公式及前n项和;
的通项公式及前n项和;(3)记集合
 ,若M的子集个数为16,求实数
,若M的子集个数为16,求实数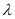 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=lg
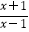 ,g(x)=ex+
,g(x)=ex+  ,则 ( )
,则 ( )
A.f(x)与g(x)都是奇函数
B.f(x)是奇函数,g(x)是偶函数
C.f(x)与g(x)都是偶函数
D.f(x)是偶函数,g(x)是奇函数
相关试题

