【题目】已知 ![]() 和
和 ![]() 是平面内互相垂直的两条直线,它们的交点为A,异于点A的两动点B、C分别在
是平面内互相垂直的两条直线,它们的交点为A,异于点A的两动点B、C分别在 ![]() 、
、 ![]() 上,且BC=
上,且BC= ![]() ,则过A、B、C三点圆的面积为( )
,则过A、B、C三点圆的面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】B
【解析】解答:由题意,l1和l2是平面内互相垂直的两条直线,它们的交点为A,BC=3,∴过A、B、C三点的动圆的圆心轨迹是以A为圆心, ![]() 为半径的圆,∵过A、B、C三点的动圆的圆的半径为
为半径的圆,∵过A、B、C三点的动圆的圆的半径为 ![]() ,∴过A、B、C三点的动圆上的点到点A的距离为3,∴过A、B、C三点的动圆所形成的图形是以A为圆心,3为半径的圆,∴过A、B、C三点的动圆所形成的图形面积为9π.故选:B.分析:本题主要考查了轨迹方程,解决问题的关键是通过所给条件分析得到圆心坐标及半径,然后求得圆的面积即可.
,∴过A、B、C三点的动圆上的点到点A的距离为3,∴过A、B、C三点的动圆所形成的图形是以A为圆心,3为半径的圆,∴过A、B、C三点的动圆所形成的图形面积为9π.故选:B.分析:本题主要考查了轨迹方程,解决问题的关键是通过所给条件分析得到圆心坐标及半径,然后求得圆的面积即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=x+b与曲线
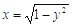 有且只有一个交点,则
有且只有一个交点,则 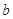 的取值范围是 ( )
的取值范围是 ( )
A.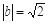
B.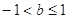 或
或 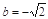
C.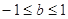 或
或 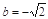
D.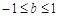
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆锥曲线C的极坐标方程为ρ2=
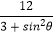 ,F1是圆锥曲线C的左焦点.直线l:
,F1是圆锥曲线C的左焦点.直线l: 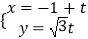 (t为参数).
(t为参数).
(1)求圆锥曲线C的直角坐标方程和直线l的直角坐标方程;
(2)若直线l与圆锥曲线C交于M,N两点,求|F1M|+|F1N|. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x|,g(x)=﹣|x﹣4|+m.
(1)解关于x的不等式g[f(x)]+3﹣m>0;
(2)若函数f(x)的图象恒在函数g(2x)图象的上方,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.
(1)求f(4)与f(8)的值;
(2)解不等式f(x)﹣f(x﹣2)>3. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的函数f(x)=2|x﹣m|﹣1(m为实数)为偶函数,记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为( )
A.a<b<c
B.c<a<b
C.a<c<b
D.c<b<a -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:三棱锥
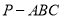 中,侧面
中,侧面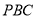 垂直底面,
垂直底面, 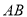 是底面最长的边;图1是三棱锥
是底面最长的边;图1是三棱锥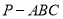 的三视图,其中的侧视图和俯视图均为直角三角形;图2是用斜二测画法画出的三棱锥
的三视图,其中的侧视图和俯视图均为直角三角形;图2是用斜二测画法画出的三棱锥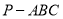 的直观图的一部分,其中点
的直观图的一部分,其中点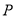 在
在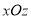 平面内.
平面内.(Ⅰ)请在图2中将三棱锥
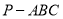 的直观图补充完整,并指出三棱锥
的直观图补充完整,并指出三棱锥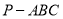 的哪些面是直角三角形;
的哪些面是直角三角形;

(Ⅱ)设二面角
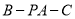 的大小为
的大小为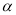 ,求
,求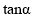 的值;
的值;(Ⅲ)求点
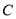 到面
到面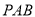 的距离.
的距离.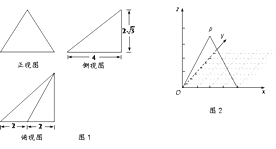
相关试题

