【题目】已知在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆锥曲线C的极坐标方程为ρ2= ![]() ,F1是圆锥曲线C的左焦点.直线l:
,F1是圆锥曲线C的左焦点.直线l: ![]() (t为参数).
(t为参数).
(1)求圆锥曲线C的直角坐标方程和直线l的直角坐标方程;
(2)若直线l与圆锥曲线C交于M,N两点,求|F1M|+|F1N|.
参考答案:
【答案】
(1)解:∵ρsinθ=y,ρ2= ![]() ,
,
∴ρ2sin2θ+3ρ2=12,
∴y2+3x2+3y2=12,
∴ ![]()
∴圆锥曲线c的普通方程为 ![]() ,
,
由直线l: ![]() (t为参数),消t得
(t为参数),消t得 ![]() ,
,
所以直线l的直角坐标方程 ![]() ,
,
(2)解:将直线l的参数方程 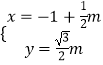 (m为参数),代入椭圆方程得:5m2﹣4m﹣12=0,
(m为参数),代入椭圆方程得:5m2﹣4m﹣12=0,
所以,m1+m2= ![]() ,m1m2=﹣
,m1m2=﹣ ![]() ,
,
所以,|F1M|+|F1N|=|m1|+|m2|=|m1﹣m2|= ![]() =
= ![]()
【解析】(1)根据极坐标和直角坐标以及参数方程的定义即可求出;(2)先化为参数方程,再根据韦达定理即可求出|F1M|+|F1N|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知已知圆
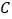 经过
经过  、
、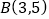 两点,且圆心C在直线
两点,且圆心C在直线 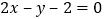 上,求解:(1)圆C的方程;(2)若直线
上,求解:(1)圆C的方程;(2)若直线  与圆
与圆 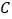 总有公共点,求实数
总有公共点,求实数  的取值范围.
的取值范围.
(1)求圆C的方程;
(2)若直线 与圆
与圆  总有公共点,求实数
总有公共点,求实数 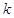 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角△ABC中,AB⊥BC,D为BC边上异于B、C的一点,以AB为直径作⊙O,并分别交AC,AD于点E,F.
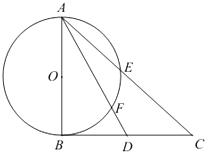
(1)证明:C,E,F,D四点共圆;
(2)若D为BC的中点,且AF=3,FD=1,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=x+b与曲线
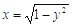 有且只有一个交点,则
有且只有一个交点,则 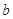 的取值范围是 ( )
的取值范围是 ( )
A.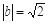
B.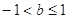 或
或 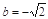
C.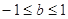 或
或 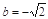
D.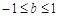
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x|,g(x)=﹣|x﹣4|+m.
(1)解关于x的不等式g[f(x)]+3﹣m>0;
(2)若函数f(x)的图象恒在函数g(2x)图象的上方,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
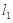 和
和  是平面内互相垂直的两条直线,它们的交点为A,异于点A的两动点B、C分别在
是平面内互相垂直的两条直线,它们的交点为A,异于点A的两动点B、C分别在 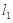 、
、  上,且BC=
上,且BC= 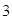 ,则过A、B、C三点圆的面积为( )
,则过A、B、C三点圆的面积为( )
A.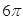
B.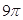
C.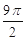
D.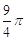
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.
(1)求f(4)与f(8)的值;
(2)解不等式f(x)﹣f(x﹣2)>3.
相关试题

