【题目】直线y=x+b与曲线 ![]() 有且只有一个交点,则
有且只有一个交点,则 ![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]()
B.![]() 或
或 ![]()
C.![]() 或
或 ![]()
D.![]()
参考答案:
【答案】B
【解析】解答:由 ![]() ,可得,曲线方程表示一个在y轴右边的单位圆的一半, 则圆心坐标为(0,0),圆的半径r=1,
,可得,曲线方程表示一个在y轴右边的单位圆的一半, 则圆心坐标为(0,0),圆的半径r=1,
画出相应的图形,如图所示: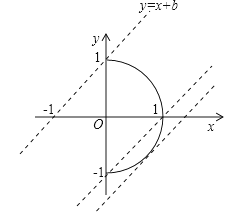
∵当直线y=x+b过(0,-1)时,把(0,-1)代入直线方程得:b=-1,
当直线y=x+b过(0,1)时,把(0,1)代入直线方程得:b=1,
∴当-1<b≤1时,直线y=x+b与半圆只有一个交点时,
又直线y=x+b与半圆相切时,圆心到直线的距离d=r,即 ![]() ,
,
解得:b= ![]() (舍去)或b=-
(舍去)或b=- ![]() ,
,
综上,直线与曲线只有一个交点时,b的取值范围为-1<b≤1或b=- ![]() .故选B
.故选B
分析:本题主要考查了直线与圆相交的性质,解决问题的关键是根据直线与圆的交点个数进行分析,利用待定系数法确定一次函数解析式,以及点到直线的距离公式;利用了数形结合的思想,根据题意得出此曲线表示在y轴右边的单位圆的一半,并画出相应的图形是解本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
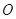 的圆心为原点
的圆心为原点 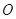 ,且与直线
,且与直线 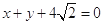 相切。
相切。 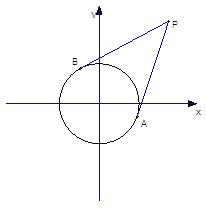
(1)求圆 的方程;
的方程;
(2)过点 (8,6)引圆O的两条切线
(8,6)引圆O的两条切线 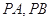 ,切点为
,切点为 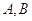 ,求直线
,求直线 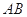 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知已知圆
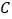 经过
经过  、
、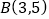 两点,且圆心C在直线
两点,且圆心C在直线 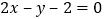 上,求解:(1)圆C的方程;(2)若直线
上,求解:(1)圆C的方程;(2)若直线  与圆
与圆 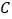 总有公共点,求实数
总有公共点,求实数  的取值范围.
的取值范围.
(1)求圆C的方程;
(2)若直线 与圆
与圆  总有公共点,求实数
总有公共点,求实数 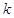 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角△ABC中,AB⊥BC,D为BC边上异于B、C的一点,以AB为直径作⊙O,并分别交AC,AD于点E,F.
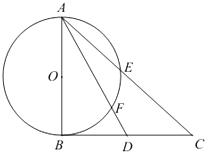
(1)证明:C,E,F,D四点共圆;
(2)若D为BC的中点,且AF=3,FD=1,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆锥曲线C的极坐标方程为ρ2=
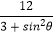 ,F1是圆锥曲线C的左焦点.直线l:
,F1是圆锥曲线C的左焦点.直线l: 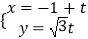 (t为参数).
(t为参数).
(1)求圆锥曲线C的直角坐标方程和直线l的直角坐标方程;
(2)若直线l与圆锥曲线C交于M,N两点,求|F1M|+|F1N|. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x|,g(x)=﹣|x﹣4|+m.
(1)解关于x的不等式g[f(x)]+3﹣m>0;
(2)若函数f(x)的图象恒在函数g(2x)图象的上方,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
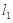 和
和  是平面内互相垂直的两条直线,它们的交点为A,异于点A的两动点B、C分别在
是平面内互相垂直的两条直线,它们的交点为A,异于点A的两动点B、C分别在 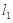 、
、  上,且BC=
上,且BC= 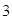 ,则过A、B、C三点圆的面积为( )
,则过A、B、C三点圆的面积为( )
A.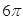
B.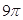
C.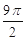
D.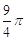
相关试题

