【题目】如果存在函数![]() (
(![]() 为常数),使得对函数
为常数),使得对函数![]() 定义域内任意
定义域内任意![]() 都有
都有![]() 成立,那么称
成立,那么称![]() 为函数
为函数![]() 的一个“线性覆盖函数”.给出如下四个结论:
的一个“线性覆盖函数”.给出如下四个结论:
①函数![]() 存在“线性覆盖函数”;
存在“线性覆盖函数”;
②对于给定的函数![]() ,其“线性覆盖函数”可能不存在,也可能有无数个;
,其“线性覆盖函数”可能不存在,也可能有无数个;
③![]() 为函数
为函数![]() 的一个“线性覆盖函数”;
的一个“线性覆盖函数”;
④若![]() 为函数
为函数![]() 的一个“线性覆盖函数”,则
的一个“线性覆盖函数”,则![]()
其中所有正确结论的序号是___________
参考答案:
【答案】②③
【解析】对①:由函数![]() 的图象可知,不存在“线性覆盖函数”故命题①错误
的图象可知,不存在“线性覆盖函数”故命题①错误
对②:如f(x)=sinx,则g(x)=B(B<﹣1)就是“线性覆盖函数”,且有无数个,再如①中的函数![]() 就没有“线性覆盖函数”,∴命题②正确;
就没有“线性覆盖函数”,∴命题②正确;
对③:设![]() 则
则![]()
当![]() 时,
时, ![]() 在(0,1)单调递增
在(0,1)单调递增
当![]() 时,
时, ![]() 在
在![]() 单调递减
单调递减
![]() ,即
,即![]()
![]() 为函数
为函数![]() 的一个“线性覆盖函数”;命题③正确
的一个“线性覆盖函数”;命题③正确
对④,设![]() ,则
,则![]() ,当b=1时,
,当b=1时, ![]() 也为函数
也为函数![]() 的一个“线性覆盖函数”,故命题④错误
的一个“线性覆盖函数”,故命题④错误
故答案为②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】现在颈椎病患者越来越多,甚至大学生也出现了颈椎病,年轻人患颈椎病多与工作、生活方式有关,某调查机构为了了解大学生患有颈椎病是否与长期过度使用电子产品有关,在遂宁市中心医院随机的对入院的50名大学生进行了问卷调查,得到了如下的4×4列联表:
未过度使用
过度使用
合计
未患颈椎病
15
5
20
患颈椎病
10
20
30
合计
25
25
50
(1)是否有99.5%的把握认为大学生患颈锥病与长期过度使用电子产品有关?
(2)已知在患有颈锥病的10名未过度使用电子产品的大学生中,有3名大学生又患有肠胃炎,现在从上述的10名大学生中,抽取3名大学生进行其他方面的排查,记选出患肠胃炎的学生人数为
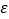 ,求
,求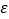 的分布列及数学期望.
的分布列及数学期望.参考数据与公式:
P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
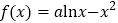 .
.(1)当
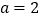 时,求函数
时,求函数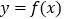 在
在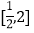 上的最大值;
上的最大值;(2)令
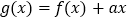 ,若
,若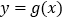 在区间
在区间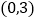 上为单调递增函数,求
上为单调递增函数,求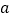 的取值范围;
的取值范围;(3)当
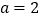 时,函数
时,函数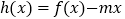 的图象与
的图象与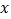 轴交于两点
轴交于两点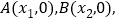 且
且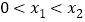 ,又
,又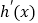 是
是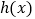 的导函数.若正常数
的导函数.若正常数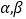 满足条件
满足条件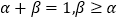 .证明:
.证明: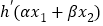 <0.
<0. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有30名男职员和20名女职员,公司进行了一次全员参与的职业能力测试,现随机询问了该公司5名男职员和5名女职员在测试中的成绩(满分为30分),可知这5名男职员的测试成绩分别为16,24,18,
22,20,5名女职员的测试成绩分别为18,23,23,18,23,则下列说法一定正确的是( )
A. 这种抽样方法是分层抽样
B. 这种抽样方法是系统抽样
C. 这5名男职员的测试成绩的方差大于这5名女职员的测试成绩的方差
D. 该测试中公司男职员的测试成绩的平均数小于女职员的测试成绩的平均数
-
科目: 来源: 题型:
查看答案和解析>>【题目】有
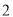 名男生,
名男生, 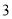 名女生,在下列不同条件下,求不同的排列方法种数.(最后结果化成数
名女生,在下列不同条件下,求不同的排列方法种数.(最后结果化成数字)
(1)排成前后两排,前排
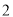 人,后排
人,后排 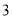 人;
人; (2)全体排成一排,甲不站在排头也不站在排尾;
(3)全体排成一排,女生必须站在一起;
(4)全体排成一排,男生不能相邻.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
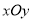 中,
中, 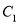 的参数方程为
的参数方程为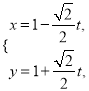 (
(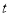 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,  轴正半轴为极轴的极坐标系中,
轴正半轴为极轴的极坐标系中, 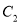 的极坐标方程
的极坐标方程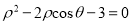 .
.(Ⅰ)说明
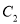 是哪种曲线,并将
是哪种曲线,并将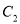 的方程化为普通方程;
的方程化为普通方程;(Ⅱ)
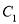 与
与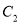 有两个公共点
有两个公共点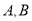 ,顶点
,顶点 的极坐标
的极坐标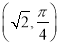 ,求线段
,求线段 的长及定点
的长及定点 到
到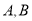 两点的距离之积.
两点的距离之积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
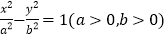 的实轴端点分别为
的实轴端点分别为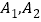 ,记双曲线的其中一个焦点为
,记双曲线的其中一个焦点为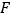 ,一个虚轴端点为
,一个虚轴端点为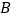 ,若在线段
,若在线段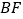 上(不含端点)有且仅有两个不同的点
上(不含端点)有且仅有两个不同的点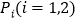 ,使得
,使得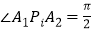 ,则双曲线的离心率
,则双曲线的离心率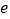 的取值范围是( )
的取值范围是( )A.
 B.
B. 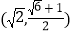 C.
C. 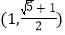 D.
D. 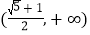
相关试题

