【题目】有 ![]() 名男生,
名男生, ![]() 名女生,在下列不同条件下,求不同的排列方法种数.(最后结果化成数
名女生,在下列不同条件下,求不同的排列方法种数.(最后结果化成数
字)
(1)排成前后两排,前排 ![]() 人,后排
人,后排 ![]() 人;
人;
(2)全体排成一排,甲不站在排头也不站在排尾;
(3)全体排成一排,女生必须站在一起;
(4)全体排成一排,男生不能相邻.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .
.
【解析】试题分析:(1)根据题意,将5人全排列即可,由排列数公式计算可得答案;
(2)根据题意,分2步进行分析:先分析甲,再将其余4人全排列,分别求出每一步的情况数目,由分步计数原理计算可得答案;
(3)根据题意,用插空法分2步进行分析:先将女生看成一个整体,考虑女生之间的顺序,再将女生的整体与2名男生在一起进行全排列,分别求出每一步的情况数目,由分步计数原理计算可得答案;
(4)根据题意,用插空法分析:先将3名女生全排列,再在女生之间及首尾空出的4个空位中任选2个空位排男生,分别求出每一步的情况数目,由分步计数原理计算可得答案.
试题解析:
(1) 分两步,第一步先从 ![]() 人中任意选出
人中任意选出 ![]() 人,第二步将这
人,第二步将这 ![]() 人排成一排.利用乘法计数原理,得到排法种数为
人排成一排.利用乘法计数原理,得到排法种数为 ![]() .
.
(2) 分两步,先从 ![]() 人中任意选出
人中任意选出 ![]() 人,再排成一排,有
人,再排成一排,有 ![]() 种方法.第二步给其余
种方法.第二步给其余 ![]() 人在后排(确定)排成一排,有
人在后排(确定)排成一排,有 ![]() 种排法.利用乘法计数原理,共有
种排法.利用乘法计数原理,共有 ![]() 种排法.
种排法.
(3) 分两步,首先从甲以外的 ![]() 人中选
人中选 ![]() 人站在排头与排尾,有
人站在排头与排尾,有 ![]() 种方法,其次连同甲的
种方法,其次连同甲的 ![]() 人在中间排成一排,有
人在中间排成一排,有 ![]() 种方法.利用乘法计数原理,有
种方法.利用乘法计数原理,有 ![]() 种排法.或先将甲放在中间
种排法.或先将甲放在中间 ![]() 个位置,有
个位置,有 ![]() 种方法,其次将连同甲的
种方法,其次将连同甲的 ![]() 人排成一排,共
人排成一排,共 ![]() 种方法,利用乘法计数原理,则共有
种方法,利用乘法计数原理,则共有 ![]() 种方法.
种方法.
(4) 分两步,首先将女生排在一起当成一个元素(捆绑法)并与其他 ![]() 个男生共
个男生共 ![]() 个元素排成
个元素排成
排,有 ![]() 种方法,再将
种方法,再将 ![]() 名女生排成一排,共
名女生排成一排,共 ![]() 种方法,利用乘法计数原理,共有
种方法,利用乘法计数原理,共有 ![]() 种方法.
种方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
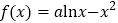 .
.(1)当
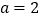 时,求函数
时,求函数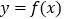 在
在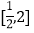 上的最大值;
上的最大值;(2)令
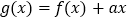 ,若
,若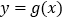 在区间
在区间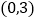 上为单调递增函数,求
上为单调递增函数,求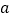 的取值范围;
的取值范围;(3)当
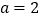 时,函数
时,函数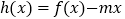 的图象与
的图象与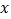 轴交于两点
轴交于两点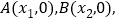 且
且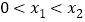 ,又
,又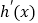 是
是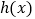 的导函数.若正常数
的导函数.若正常数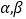 满足条件
满足条件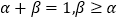 .证明:
.证明: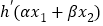 <0.
<0. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有30名男职员和20名女职员,公司进行了一次全员参与的职业能力测试,现随机询问了该公司5名男职员和5名女职员在测试中的成绩(满分为30分),可知这5名男职员的测试成绩分别为16,24,18,
22,20,5名女职员的测试成绩分别为18,23,23,18,23,则下列说法一定正确的是( )
A. 这种抽样方法是分层抽样
B. 这种抽样方法是系统抽样
C. 这5名男职员的测试成绩的方差大于这5名女职员的测试成绩的方差
D. 该测试中公司男职员的测试成绩的平均数小于女职员的测试成绩的平均数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果存在函数
 (
( 为常数),使得对函数
为常数),使得对函数 定义域内任意
定义域内任意 都有
都有 成立,那么称
成立,那么称 为函数
为函数 的一个“线性覆盖函数”.给出如下四个结论:
的一个“线性覆盖函数”.给出如下四个结论:①函数
 存在“线性覆盖函数”;
存在“线性覆盖函数”;②对于给定的函数
 ,其“线性覆盖函数”可能不存在,也可能有无数个;
,其“线性覆盖函数”可能不存在,也可能有无数个;③
 为函数
为函数 的一个“线性覆盖函数”;
的一个“线性覆盖函数”;④若
 为函数
为函数 的一个“线性覆盖函数”,则
的一个“线性覆盖函数”,则
其中所有正确结论的序号是___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
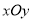 中,
中, 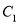 的参数方程为
的参数方程为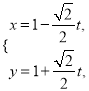 (
(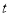 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点, 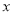 轴正半轴为极轴的极坐标系中,
轴正半轴为极轴的极坐标系中, 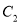 的极坐标方程
的极坐标方程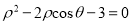 .
.(Ⅰ)说明
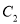 是哪种曲线,并将
是哪种曲线,并将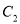 的方程化为普通方程;
的方程化为普通方程;(Ⅱ)
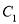 与
与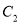 有两个公共点
有两个公共点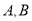 ,顶点
,顶点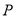 的极坐标
的极坐标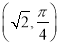 ,求线段
,求线段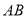 的长及定点
的长及定点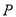 到
到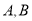 两点的距离之积.
两点的距离之积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
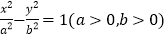 的实轴端点分别为
的实轴端点分别为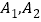 ,记双曲线的其中一个焦点为
,记双曲线的其中一个焦点为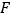 ,一个虚轴端点为
,一个虚轴端点为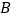 ,若在线段
,若在线段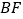 上(不含端点)有且仅有两个不同的点
上(不含端点)有且仅有两个不同的点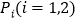 ,使得
,使得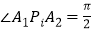 ,则双曲线的离心率
,则双曲线的离心率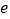 的取值范围是( )
的取值范围是( )A.
 B.
B. 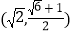 C.
C. 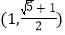 D.
D. 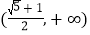
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
年 份
2008
2009
2010
2011
2012
2013
2014
年份代号t
1
2
3
4
5
6
7
人均纯收入y
2.7
3.6
3.3
4.6
5.4
5.7
6.2
对变量t与y进行相关性检验,得知t与y之间具有线性相关关系.
(1)求y关于t的线性回归方程;
(2)预测该地区2017年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
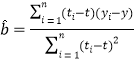 ,
,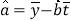
相关试题

