【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在区间
在区间![]() 上为单调递增函数,求
上为单调递增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() 且
且![]() ,又
,又![]() 是
是![]() 的导函数.若正常数
的导函数.若正常数![]() 满足条件
满足条件![]() .证明:
.证明:![]() <0.
<0.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() ,理由见解析
,理由见解析
【解析】试题分析:(1)![]() ,可知
,可知![]() 在[
在[![]() ,1]是增函数,在[1,2]是减函数,所以最大值为f(1).(2)
,1]是增函数,在[1,2]是减函数,所以最大值为f(1).(2)![]() 在区间
在区间![]() 上为单调递增函数,即
上为单调递增函数,即![]() 在
在![]() 上恒成立。
上恒成立。![]() ,利用分离参数
,利用分离参数![]() 在
在![]() 上恒成立,即求
上恒成立,即求![]() 的最大值。
的最大值。
(3)![]() 有两个实根
有两个实根![]() ,
, ![]() ,两式相减
,两式相减![]() ,又
,又![]() ,
,![]()
![]() .要证:
.要证:![]() ,只需证:
,只需证:![]() ,令
,令![]() 可证。
可证。
试题解析:(1) ![]()
函数![]() 在[
在[![]() ,1]是增函数,在[1,2]是减函数,
,1]是增函数,在[1,2]是减函数,
所以![]() .
.
(2)因为![]() ,所以
,所以![]() ,
,
因为![]() 在区间
在区间![]() 单调递增函数,所以
单调递增函数,所以![]() 在(0,3)恒成立
在(0,3)恒成立
![]() ,有
,有![]() =
=![]() ,(
,(![]() )
)
综上:![]()
(3)∵![]() ,又
,又![]() 有两个实根
有两个实根![]() ,
,
∴![]() ,两式相减,得
,两式相减,得![]() ,
,
∴![]() ,
,
于是![]()
![]() .
.
![]()
要证:![]() ,只需证:
,只需证:![]()
只需证:![]() .(*)
.(*)
令![]() ,∴(*)化为
,∴(*)化为 ![]() ,只证
,只证![]() 即可.
即可.
![]() 在(0,1)上单调递增,
在(0,1)上单调递增,![]() ,
,
即![]() .∴
.∴![]() .
.
(其他解法根据情况酌情给分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益
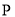 与投入
与投入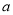 (单位:万元)满足
(单位:万元)满足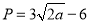 ,乙城市收益
,乙城市收益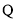 与投入
与投入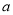 (单位:万元)满足
(单位:万元)满足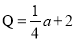 ,设甲城市的投入为
,设甲城市的投入为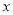 (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为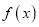 (单位:万元)。
(单位:万元)。(1)当甲城市投资50万元时,求此时公司总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
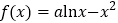 .
.(1)当
 时,求函数
时,求函数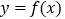 在
在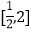 上的最大值;
上的最大值;(2)令
 ,若
,若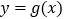 在区间
在区间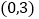 上为单调递增函数,求
上为单调递增函数,求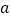 的取值范围;
的取值范围;(3)当
 时,函数
时,函数 的图象与
的图象与 轴交于两点
轴交于两点 且
且 ,又
,又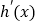 是
是 的导函数.若正常数
的导函数.若正常数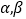 满足条件
满足条件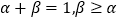 .证明:
.证明: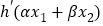 <0.
<0. -
科目: 来源: 题型:
查看答案和解析>>【题目】现在颈椎病患者越来越多,甚至大学生也出现了颈椎病,年轻人患颈椎病多与工作、生活方式有关,某调查机构为了了解大学生患有颈椎病是否与长期过度使用电子产品有关,在遂宁市中心医院随机的对入院的50名大学生进行了问卷调查,得到了如下的4×4列联表:
未过度使用
过度使用
合计
未患颈椎病
15
5
20
患颈椎病
10
20
30
合计
25
25
50
(1)是否有99.5%的把握认为大学生患颈锥病与长期过度使用电子产品有关?
(2)已知在患有颈锥病的10名未过度使用电子产品的大学生中,有3名大学生又患有肠胃炎,现在从上述的10名大学生中,抽取3名大学生进行其他方面的排查,记选出患肠胃炎的学生人数为
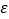 ,求
,求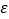 的分布列及数学期望.
的分布列及数学期望.参考数据与公式:
P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有30名男职员和20名女职员,公司进行了一次全员参与的职业能力测试,现随机询问了该公司5名男职员和5名女职员在测试中的成绩(满分为30分),可知这5名男职员的测试成绩分别为16,24,18,
22,20,5名女职员的测试成绩分别为18,23,23,18,23,则下列说法一定正确的是( )
A. 这种抽样方法是分层抽样
B. 这种抽样方法是系统抽样
C. 这5名男职员的测试成绩的方差大于这5名女职员的测试成绩的方差
D. 该测试中公司男职员的测试成绩的平均数小于女职员的测试成绩的平均数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果存在函数
 (
( 为常数),使得对函数
为常数),使得对函数 定义域内任意
定义域内任意 都有
都有 成立,那么称
成立,那么称 为函数
为函数 的一个“线性覆盖函数”.给出如下四个结论:
的一个“线性覆盖函数”.给出如下四个结论:①函数
 存在“线性覆盖函数”;
存在“线性覆盖函数”;②对于给定的函数
 ,其“线性覆盖函数”可能不存在,也可能有无数个;
,其“线性覆盖函数”可能不存在,也可能有无数个;③
 为函数
为函数 的一个“线性覆盖函数”;
的一个“线性覆盖函数”;④若
 为函数
为函数 的一个“线性覆盖函数”,则
的一个“线性覆盖函数”,则
其中所有正确结论的序号是___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】有
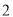 名男生,
名男生, 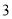 名女生,在下列不同条件下,求不同的排列方法种数.(最后结果化成数
名女生,在下列不同条件下,求不同的排列方法种数.(最后结果化成数字)
(1)排成前后两排,前排
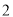 人,后排
人,后排 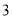 人;
人; (2)全体排成一排,甲不站在排头也不站在排尾;
(3)全体排成一排,女生必须站在一起;
(4)全体排成一排,男生不能相邻.
相关试题

