【题目】已知函数f(x)=sinωxcosωx﹣ ![]() (ω>0)图象的两条相邻对称轴为
(ω>0)图象的两条相邻对称轴为 ![]() .
.
(1)求函数y=f(x)的对称轴方程;
(2)若函数y=f(x)﹣ ![]() 在(0,π)上的零点为x1 , x2 , 求cos(x1﹣x2)的值.
在(0,π)上的零点为x1 , x2 , 求cos(x1﹣x2)的值.
参考答案:
【答案】
(1)解:函数 ![]()
化简可得f(x)= ![]() =
= ![]()
由题意可得周期T=π,
∴ ![]()
∴ ![]()
故函数y=f(x)的对称轴方程为 ![]()
即 ![]()
(2)解:由函数y=f(x)﹣ ![]() 在(0,π)上的零点为x1,x2,
在(0,π)上的零点为x1,x2,
可知 ![]() ,
,
且 ![]() .
.
易知(x1,f(x1))与(x2,f(x2))关于 ![]() 对称,
对称,
则 ![]() ,
,
∴ ![]() =
= ![]() =sin(2
=sin(2 ![]() )=
)= ![]() .
.
【解析】(1)利用二倍角和辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,根据两条相邻对称轴为 ![]() .求解出ω,即可求解对称轴方程.(2)利用零点为x1 , x2 , 求解x1 , x2的对称轴.即可求cos(x1﹣x2)的值.
.求解出ω,即可求解对称轴方程.(2)利用零点为x1 , x2 , 求解x1 , x2的对称轴.即可求cos(x1﹣x2)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,为了测量A,B处岛屿的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为( )

A. 海里
海里
B. 海里
海里
C. 海里
海里
D.40海里 -
科目: 来源: 题型:
查看答案和解析>>【题目】候鸟每年都要随季节的变化而进行大规模地迁徙,研究某种鸟类的专家发现,该种鸟类的飞行速度v(单位:m/s)与其耗氧量M之间的关系为:
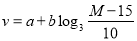 ,(其中a,b是实数),据统计,该种鸟类在静止的时间其耗氧量为45个单位,而其耗氧量为105个单位时,其飞行速度为1m/s.
,(其中a,b是实数),据统计,该种鸟类在静止的时间其耗氧量为45个单位,而其耗氧量为105个单位时,其飞行速度为1m/s.(1)求出a,b的值;
(2)若这种鸟类为赶路程,飞行的速度不能低于2m/s,则其耗氧量至少要多少个单位。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
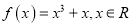 .
.(1)判断函数
 的奇偶性;
的奇偶性;(2)是否存在这样的实数
 ,使
,使 对所有的
对所有的 均成立?若存在,求出适合条件的实数
均成立?若存在,求出适合条件的实数 的值或范围;若不存在,说明理由.
的值或范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着我国经济模式的改变,电商已成为当今城乡种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出
 吨该商品可获利润
吨该商品可获利润 万元,未售出的商品,每吨亏损
万元,未售出的商品,每吨亏损 万元根据往年的销售资料,得到该商品一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了
万元根据往年的销售资料,得到该商品一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了 吨该商品,现以
吨该商品,现以 单位:吨,
单位:吨, )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量, (单位:万 元)表示该电商下“个销售季度内经销该商品获得的利润.
(单位:万 元)表示该电商下“个销售季度内经销该商品获得的利润.
(1)视
 分布在各区间内的频率为相应的概率,求
分布在各区间内的频率为相应的概率,求 ;
;(2)将
 表示为
表示为 的函数,求出该函数表达式;
的函数,求出该函数表达式;(3)在频率分布直方图的市场需求量分组中,若以市场需求量落入该区间的频率作为市场需求量的概率,求该季度利润不超过
 万元的概率.
万元的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—4:坐标系与参数方程
在直角坐标系xOy中,设倾斜角为α的直线l:
 (t为参数)与曲线C:
(t为参数)与曲线C: (θ为参数)相交于不同的两点A,B.
(θ为参数)相交于不同的两点A,B.(Ⅰ)若α=
 ,求线段AB中点M的坐标;
,求线段AB中点M的坐标;(Ⅱ)若|PA|·|PB|=|OP|
 ,其中P(2,
,其中P(2, ),求直线l的斜率.
),求直线l的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国古代第一部数学专著,成于公元一世纪左右,系统总结了战国、秦、汉时期的数学成就.其中《方田》一章中记载了计算弧田(弧田就是由圆弧和其所对弦所围成弓形)的面积所用的经验公式:弧田面积=
 (弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为
(弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为 ,弦长为
,弦长为 的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中
的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中 ,
, )
)A. 15 B. 16 C. 17 D. 18
相关试题

