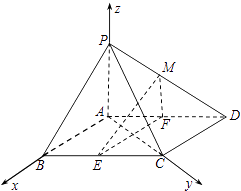
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上. 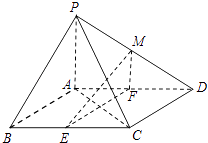
(1)求证:EF⊥平面PAC;
(2)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求 ![]() 的值.
的值.
参考答案:
【答案】
(1)证明:∵在平行四边形ABCD中,∠BCD=135°,∴∠ABC=45°,
∵AB=AC,∴AB⊥AC.
∵E,F分别为BC,AD的中点,∴EF∥AB,
∴EF⊥AC.
∵侧面PAB⊥底面ABCD,且∠BAP=90°,
∴PA⊥底面ABCD.
又EF底面ABCD,
∴PA⊥EF.
又∵PA∩AC=A,PA平面PAC,AC平面PAC,
∴EF⊥平面PAC.
(2)解:∵PA⊥底面ABCD,AB⊥AC,∴AP,AB,AC两两垂直,
以A为原点,分别以AB,AC,AP为x轴、y轴和z轴建立空间直角坐标系如图:
则A(0,0,0),B(2,0,0),C(0,2,0),P(0,0,2),D(﹣2,2,0),E(1,1,0),
∴ ![]() =(2,0,﹣2),
=(2,0,﹣2), ![]() =(﹣2,2,﹣2),
=(﹣2,2,﹣2), ![]() ,
, ![]() =(1,1,﹣2).
=(1,1,﹣2).
设 ![]() =λ(0≤λ≤1),则
=λ(0≤λ≤1),则 ![]() =(﹣2λ,2λ,﹣2λ),
=(﹣2λ,2λ,﹣2λ),
∴ ![]() =
= ![]() -
- ![]() =(1+2λ,1﹣2λ,2λ﹣2),
=(1+2λ,1﹣2λ,2λ﹣2),
显然平面ABCD的一个法向量为 ![]() =(0,0,1).
=(0,0,1).
设平面PBC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 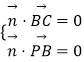 ,即
,即 ![]()
令x=1,得 ![]() =(1,1,1).
=(1,1,1).
∴cos< ![]() ,
, ![]() >=
>= 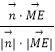 =
= ![]() ,cos<
,cos< ![]() >=
>= 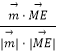 =
= ![]() .
.
∵直线ME与平面PBC所成的角和此直线与平面ABCD所成的角相等,
∴| ![]() |=|
|=| ![]() |,即
|,即 ![]() ,
,
解得 ![]() ,或
,或 ![]() (舍).
(舍).
∴ ![]()
![]() .
.
【解析】(1)由平行四边形的性质可得AB⊥AC,即EF⊥AC,由面面垂直的性质得出PA⊥平面ABCD,故PA⊥EF,故EF⊥平面PAC;(2)以A为原点建立空间直角坐标系,设 ![]() =λ(0≤λ≤1),求出平面PBC,平面ABCD的法向量
=λ(0≤λ≤1),求出平面PBC,平面ABCD的法向量 ![]() 及
及 ![]() 的坐标,根据线面角相等列方程解出λ.
的坐标,根据线面角相等列方程解出λ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn=2n2+n,n∈N* .
(1)求{an}的通项公式;
(2)若数列{bn}满足an=4log2bn+3,n∈N* , 求数列{anbn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】福利彩票“双色球”中红球的号码可以从01,02,03,…,32,33这33个二位号码中选取,小明利用如图所示的随机数表选取红色球的6个号码,选取方法是从第1行第9列和第10列的数字开始从左到右依次选取两个数字,则第四个被选中的红色球号码为( )
81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85
06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49
A. 12 B. 33 C. 06 D. 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费支出x与销售额y(单位:万元)之间有如下对应数据:
x
2
4
5
6
8
y
30
40
60
50
70
(1)求回归直线方程;
(2)试预测广告费支出为10万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的方程为
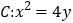 ,过点
,过点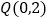 的一条直线与抛物线
的一条直线与抛物线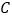 交于
交于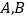 两点,若抛物线在
两点,若抛物线在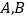 两点的切线交于点
两点的切线交于点 .
.(1)求点
 的轨迹方程;
的轨迹方程;(2)设直线
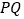 与直线
与直线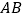 的夹角为
的夹角为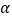 ,求
,求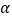 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l:y=x+1,圆O:
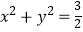 ,直线l被圆截得的弦长与椭圆C:
,直线l被圆截得的弦长与椭圆C: 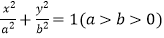 的短轴长相等,椭圆的离心率e=
的短轴长相等,椭圆的离心率e= 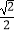 .
.
(1)求椭圆C的方程;
(2)过点M(0,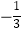 )的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过定点T?若存在,求出点T的坐标;若不存在,请说明理由.
)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过定点T?若存在,求出点T的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
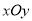 中,直线
中,直线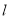 的参数方程为
的参数方程为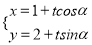 (
(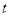 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系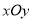 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以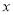 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆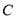 的方程为
的方程为 .
.(1)求圆
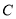 的直角坐标方程;
的直角坐标方程;(2)设圆
 与直线
与直线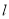 交于点
交于点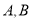 ,若点
,若点 的坐标为
的坐标为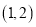 ,求
,求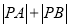 的最小值.
的最小值.
相关试题

