搜索
【题目】直线y=a分别与曲线y=2（x+1），y=x+lnx交于A、B，则|AB|的最小值为（ ）
A.3
B.2
C.
D.
参考答案：
【答案】C
【解析】解：设A（x1 ， a），B（x2 ， a），则2（x1+1）=x2+lnx2 ，
∴x1= 
（x2+lnx2）﹣1，
∴|AB|=x2﹣x1= （x2﹣lnx2）+1，
令y= （x﹣lnx）+1，则y′= （1﹣ 
），
∴函数在（0，1）上单调递减，在（1，+∞）上单调递增，
∴x=1时，函数的最小值为 
，
故选：C．
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点，需要掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值才能正确解答此题．
-
科目： 来源： 题型：
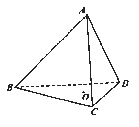
查看答案和解析>>【题目】如图，在正四面体ABCD中，
是
的中心， 
分别是
上的动点，且
．
（1）若
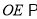平面
，求实数
的值；（2）若
，正四面体ABCD的棱长为
，求平面
和平面
所成的角余弦值． -
科目： 来源： 题型：
查看答案和解析>>【题目】设
，g（x）=ax+5﹣2a（a＞0）．
（1）求f（x）在x∈[0，1]上的值域；
（2）若对于任意x1∈[0，1]，总存在x0∈[0，1]，使得g（x0）=f（x1）成立，求a的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】某班同学利用寒假进行社会实践活动，对[25，55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：
组数
分组
低碳族人数
占本组的频率
第一组
[25，30）
120
0.6
第二组
[30，35）
195
p
第三组
[35，40）
100
0.5
第四组
[40，45）
a
0.4
第五组
[45，50）
30
0.3
第六组
[50，55）
15
0.3
（1）补全频率分布直方图并求n、a、p的值；
（2）从年龄段在[40，50）的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动，其中选取2人作为领队，求选取的2名领队中恰有1人年龄在[40，45）岁的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知定义域为R的函数f（x）=
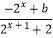是奇函数．
（1）求b的值；
（2）用定义法证明函数f（x）在R上是减函数；
（3）若对任意的t∈R，不等式f（t2﹣2t）+f（2t2﹣k）＜0恒成立，求k的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】通过对某城市一天内单次租用共享自行车的时间
分钟到
钟的
人进行统计，按照租车时间
， 
， 
， 
， 
分组做出频率分布直方图，并作出租用时间和茎叶图（图中仅列出了时间在
， 
的数据）．
（1）求
的频率分布直方图中的
；（2）从租用时间在
分钟以上（含
分钟）的人数中随机抽取
人，设随机变量
表示所抽取的
人租用时间在
内的人数，求随机变量
的分布列及数学期望． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数f（x）=x2﹣ax+a（x∈R）同时满足：
①不等式f（x）≤0的解集有且只有一个元素；
②在定义域内存在0＜x1＜x2 ， 使得不等式f（x1）＞f（x2）成立．设数列{an}的前n项和Sn=f（n）．
（1）求f（x）的表达式；
（2）求数列{an}的通项公式；
（3）设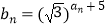
，cn=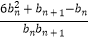 
，{cn}的前n项和为Tn ， 若Tn＞2n+t对任意n∈N，n≥2恒成立，求实数t的取值范围．
相关试题
