【题目】已知函数f(x)=cos2 ![]() ﹣sin
﹣sin ![]() cos
cos ![]() ﹣
﹣ ![]() .
.
(1)求函数f(x)的最小正周期和值域;
(2)若 ![]() ,求sin2α的值.
,求sin2α的值.
参考答案:
【答案】
(1)解:由已知,f(x)= ![]() ﹣sin
﹣sin ![]() cos
cos ![]() ﹣
﹣ ![]()
= ![]() (1+cosx)﹣
(1+cosx)﹣ ![]() sinx﹣
sinx﹣ ![]()
= ![]() cos(x+
cos(x+ ![]() ).
).
∴函数f(x)的最小正周期为2π,值域为[﹣ ![]() ,
, ![]() ].
].
(2)解:由(1)知,f(α)= ![]() cos(α+
cos(α+ ![]() )=
)= ![]() ,
,
∴cos(α+ ![]() )=
)= ![]() ,
,
∴sin2α=﹣cos( ![]() +2α)=﹣cos2(α+
+2α)=﹣cos2(α+ ![]() )
)
=1﹣2 ![]()
=1﹣ ![]()
= ![]() .
.
【解析】(1)将 ![]() 化为f(x)=
化为f(x)= ![]() cos(x+
cos(x+ ![]() )即可求得f(x)的最小正周期和值域;(2)由
)即可求得f(x)的最小正周期和值域;(2)由 ![]() 可求得cos(α+
可求得cos(α+ ![]() )=
)= ![]() ,由余弦函数的二倍角公式与诱导公式可求得sin2α的值.
,由余弦函数的二倍角公式与诱导公式可求得sin2α的值.
【考点精析】解答此题的关键在于理解二倍角的正弦公式的相关知识,掌握二倍角的正弦公式:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
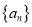 的前
的前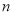 项和为
项和为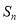 ,且
,且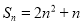 ,
, 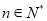 ,在数列
,在数列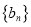 中,
中, 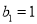 ,
, 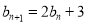 ,
, 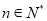 .
.(1)求证:
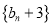 是等比数列;
是等比数列;(2)若
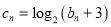 ,求数列
,求数列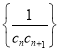 的前
的前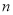 项和
项和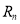 ;
;(3)求数列
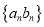 的前
的前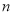 项和
项和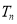 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
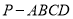 中,底面
中,底面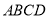 为平行四边形,
为平行四边形, 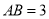 ,
, 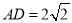 ,
, 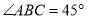 ,
, 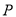 点在底面
点在底面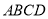 内的射影
内的射影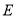 在线段
在线段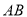 上,且
上,且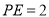 ,
, 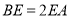 ,
, 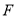 为
为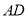 的中点,
的中点, 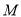 在线段
在线段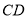 上,且
上,且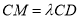 .
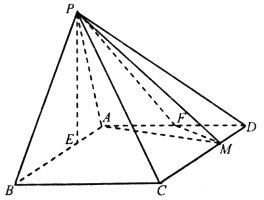
. 
(Ⅰ)当
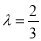 时,证明:平面
时,证明:平面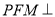 平面
平面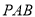 ;
;(Ⅱ)当平面
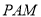 与平面
与平面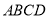 所成的二面角的正弦值为
所成的二面角的正弦值为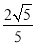 时,求四棱锥
时,求四棱锥 的体积.
的体积. -
科目: 来源: 题型:
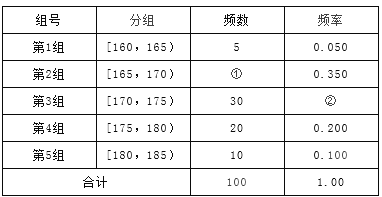
查看答案和解析>>【题目】某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下图所示.
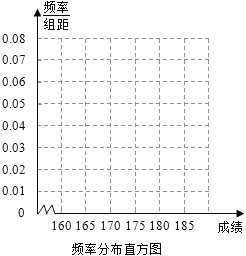
(I)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(Ⅱ)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求:第4组至少有一名学生被考官A面试的概率?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
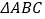 的三个内角
的三个内角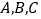 的对边长分别为
的对边长分别为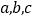 ,
,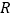 是
是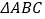 的外接圆半径,则下列四个条件
的外接圆半径,则下列四个条件(1)
 ; (2)
; (2)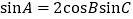 ;
;(3)
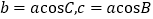 ; (4)
; (4)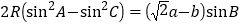 .
.有两个结论:甲:
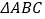 是等边三角形; 乙:
是等边三角形; 乙: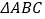 是等腰直角三角形.
是等腰直角三角形.请你选出给定的四个条件中的两个为条件,两个结论中的一个为结论,写出一个你认为正确的命题__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某运动员每次投篮命中的概率等于40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下2-组随机数:
907 966 191 925 271 932 812 458
569 683 431 257 393 027 556 488
730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
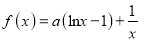 的图象与
的图象与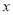 轴相切,
轴相切, 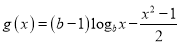 .
.(Ⅰ)求证:
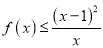 ;
;(Ⅱ)若
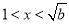 ,求证:
,求证: 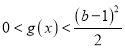
相关试题

