【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
, ![]() ,在数列
,在数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() 是等比数列;
是等比数列;
(2)若![]() ,求数列
,求数列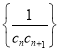 的前
的前![]() 项和
项和![]() ;
;
(3)求数列![]() 的前
的前![]() 项和
项和![]() .
.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)利用递推关系可得![]() ,由等比数列的定义即可得出结论;(2)利用对数的运算性质可得
,由等比数列的定义即可得出结论;(2)利用对数的运算性质可得![]() ,根据裂项求和方法即可得出;(3)
,根据裂项求和方法即可得出;(3)![]() 时,
时, ![]() 时,
时, ![]() ,综上
,综上![]() ,可得
,可得![]() ,再利用错位相减法及分组求和法即可得结果.
,再利用错位相减法及分组求和法即可得结果.
试题解析:(1) 证明: ![]() 且
且![]()
![]()
![]() 是首项为4,公比为2的等比数列 .
是首项为4,公比为2的等比数列 .
(2) 由(1)知 ![]() ,
,
所以 ![]() ,
,
则![]()
![]() ,
,
![]()
![]() .
.
(3) ![]() 时
时 ![]() ,
,
![]() 时
时 ![]() ,
,
综上 ![]() ,
,
![]() ,解得
,解得
![]() .
.
【方法点晴】裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,掌握一些常见的裂项技巧:①![]() ;②
;②![]()
![]() ;③
;③![]() ;
;
④![]()
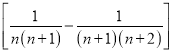 ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为
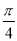 ,边界忽略不计)即为中奖·
,边界忽略不计)即为中奖·乙商场:从装有2个白球、2个蓝球和2个红球的盒子中一次性摸出1球(这些球除颜色外完全相同),它是红球的概率是
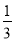 ,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.
,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.
(Ⅰ)求实数
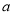 的值;
的值;(Ⅱ)试问:购买该商品的顾客在哪家商场中奖的可能性大?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<
 )的部分图象如图所示.
)的部分图象如图所示. 
(1)求函数f(x)的解析式;
(2)求函数g(x)=f(x﹣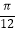 )﹣f(x+
)﹣f(x+ 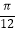 )的单调递增区间.
)的单调递增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学组织了一次高二文科学生数学学业水平模拟测试,学校从测试合格的男、女生中各随机抽取100人的成绩进行统计分析,分别制成了如图所示的男生和女生数学成绩的频率分布直方图.

(Ⅰ)若所得分数大于等于80分认定为优秀,求男、女生优秀人数各有多少人?
(Ⅱ)在(Ⅰ)中的优秀学生中用分层抽样的方法抽取5人,从这5人中任意任取2人,求至少有一名男生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
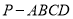 中,底面
中,底面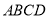 为平行四边形,
为平行四边形, 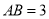 ,
, 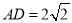 ,
, 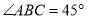 ,
, 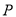 点在底面
点在底面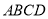 内的射影
内的射影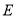 在线段
在线段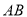 上,且
上,且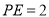 ,
, 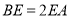 ,
, 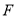 为
为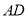 的中点,
的中点, 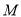 在线段
在线段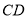 上,且
上,且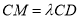 .
. 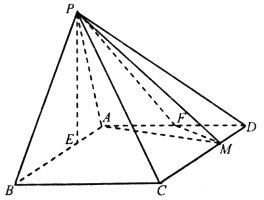
(Ⅰ)当
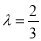 时,证明:平面
时,证明:平面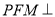 平面
平面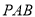 ;
;(Ⅱ)当平面
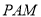 与平面
与平面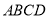 所成的二面角的正弦值为
所成的二面角的正弦值为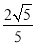 时,求四棱锥
时,求四棱锥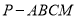 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下图所示.
(I)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(Ⅱ)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求:第4组至少有一名学生被考官A面试的概率?
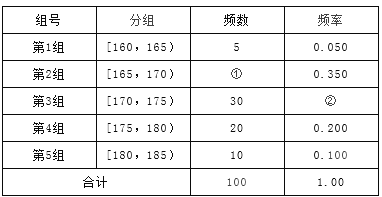
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=cos2
 ﹣sin
﹣sin  cos
cos  ﹣
﹣  .
.
(1)求函数f(x)的最小正周期和值域;
(2)若 ,求sin2α的值.
,求sin2α的值.
相关试题

