【题目】已知四棱锥![]() ,底面
,底面![]() 是
是![]() 、边长为
、边长为![]() 的菱形,又
的菱形,又![]() 底
底![]() ,且
,且![]() ,点
,点![]() 分别是棱
分别是棱![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.[
的距离.[
参考答案:
【答案】(1)详见解析(2)详见解析(3)![]()
【解析】
试题分析:(1)要证DN∥平面PMB,只要证DN∥MQ;(2)要证平面PMB⊥平面PAD,只要证MB⊥平面PAD;
(3)利用PD是三棱锥P-AMB的高PD=2,棱锥A-PMB的体积=棱锥P-AMB的体积,利用棱锥的体积公式解之
试题解析:(1)证明:取![]() 中点
中点![]() ,连接
,连接![]() ,因为
,因为![]() 分别是棱
分别是棱![]() 中点,
中点,
所以![]() ,且
,且![]() ,于是
,于是![]() ,
,
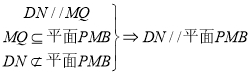 .
.
(2)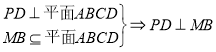 ,
,
又因为底面![]() 是
是![]() 、边长为
、边长为![]() 的菱形,且
的菱形,且![]() 为
为![]() 中点,所以
中点,所以![]() ,又
,又![]() ,
,
所以![]() .
.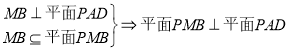 .
.
(3)因为![]() 是
是![]() 中点,所以点
中点,所以点![]() 与
与![]() 到平面
到平面![]() 等距离.过点
等距离.过点![]() 作
作![]() 于
于![]() ,由(2)由平面
,由(2)由平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
故![]() 是点
是点![]() 到平面
到平面![]() 的距离
的距离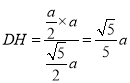 .
.
∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知圆
中,已知圆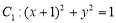 ,圆
,圆 .
.(1)若过点
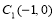 的直线
的直线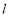 被圆
被圆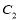 截得的弦长为
截得的弦长为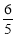 ,求直线
,求直线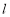 的方程;
的方程;(2)圆
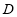 是以1为半径,圆心在圆
是以1为半径,圆心在圆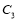 :
: 上移动的动圆 ,若圆
上移动的动圆 ,若圆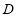 上任意一点
上任意一点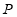 分别作圆
分别作圆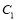 的两条切线
的两条切线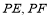 ,切点为
,切点为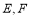 ,求
,求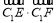 的取值范围;
的取值范围;(3)若动圆
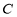 同时平分圆
同时平分圆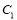 的周长、圆
的周长、圆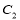 的周长,则动圆
的周长,则动圆 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1.
(1)求数列{bn}的通项公式;
(2)令cn=
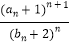 ,Tn是数列{cn}的前n项和,求证:
,Tn是数列{cn}的前n项和,求证: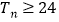
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市
 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以 ,
, ,
, ,
, ,
, ,
, ,
, 分组的频率分布直方图如图.
分组的频率分布直方图如图.
(I)求直方图中
 的值;
的值; (II)求月平均用电量的众数和中位数;
(III)在月平均用电量为
 ,
, ,
, ,
, 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取 户居民,则月平均用电量在
户居民,则月平均用电量在 的用户中应抽取多少户?
的用户中应抽取多少户? -
科目: 来源: 题型:
查看答案和解析>>【题目】正方体
 的棱长为1,
的棱长为1,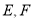 分别是棱
分别是棱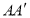 ,
, 的中点,过直线
的中点,过直线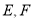 的平面分别与棱
的平面分别与棱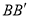 、
、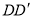 交于
交于 ,设
,设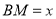 ,
,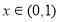 ,给出以下四个命题:
,给出以下四个命题:①四边形
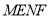 为平行四边形;
为平行四边形;②若四边形
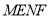 面积
面积 ,
,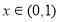 ,则
,则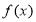 有最小值;
有最小值;③若四棱锥
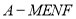 的体积
的体积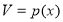
 ,
,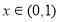 ,则
,则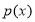 为常函数;
为常函数;④若多面体
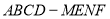 的体积
的体积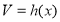 ,
,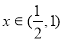 ,则
,则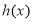 为单调函数.
为单调函数.其中假命题为( )
A.① ③ B.② C.③④ D.④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
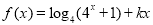 (
(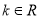 )是偶函数.
)是偶函数.(1)求
 的值;
的值;(2)设
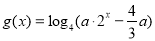 ,若函数
,若函数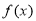 与
与 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地参加2015 年夏令营的
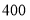 名学生的身体健康情况,将学生编号为
名学生的身体健康情况,将学生编号为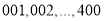 ,采用系统抽样的方法抽取一个容量为
,采用系统抽样的方法抽取一个容量为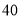 的样本,且抽到的最小号码为
的样本,且抽到的最小号码为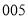 ,已知这
,已知这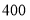 名学生分住在三个营区,从
名学生分住在三个营区,从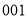 到
到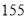 在第一营区,从
在第一营区,从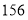 到
到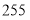 在第二营区,从
在第二营区,从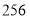 到
到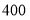 在第三营区,则第一、第二、第三营区被抽中的人数分别为( )
在第三营区,则第一、第二、第三营区被抽中的人数分别为( )A.
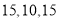 B.
B.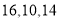
C.
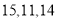 D.
D.
相关试题

