【题目】.某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图所示的频率分布直方图.

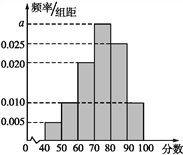
(1)求图中实数a的值;

(2)若该校高二年级共有学生640人,试估计该校高二年级期中考试数学成绩不低于60分的学生人数;

(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.

参考答案：

【答案】(1) a=0.03;(2)544;(2) P(M)=.

【解析】试题分析: （1）由频率分布直方图的性质能求出的值．
（2）先求出数学成绩不低于60分的概率，由此能求出数学成绩不低于60分的人数．
（3）数学成绩在的学生为2人，数学成绩在的学生人数为4人，由此利用列举法能求出这2名学生的数学成绩之差的绝对值大于10的槪率．

试题解析：

(1)由于图中所有小矩形的面积之和等于1，所以10×(0.005+0.01+0.02+a+0.025+0.01)=1.

解得a=0.03.

(2)根据频率分布直方图,成绩不低于60分的频率为110×(0.005+0.01)=0.85由于该校高一年级共有学生640人,利用样本估计总体的思想,可估计该校高一年级数学成绩不低于60分的人数约为640×0.85=544人 .

(3)成绩在[40,50)分数段内的人数为40×0.05=2人,分别记为A,B，成绩在[90,100]分数段内的人数为40×0.1=4人,分别记为C,D,E,F.

若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,则所有的基本事件有：(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共15种.

如果两名学生的数学成绩都在[40,50)分数段内或都在[90,100]分数段内,那么这两名学生的数学成绩之差的绝对值一定不大于10.如果一个成绩在[40,50)分数段内,另一个成绩在[90,100]分数段内，那么这两名学生的数学成绩之差的绝对值一定大于10.

记“这两名学生的数学成绩之差的绝对值不大于10”为事件M,则事件M包含的基本事件有：(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共7种.所以所求概率为P(M)=.

关闭