【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频 数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
(1)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
①假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;
②若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
参考答案:
【答案】(1) y=![]() (n∈N);(2)①76.4;②0.7.
(n∈N);(2)①76.4;②0.7.
【解析】试题分析:(Ⅰ)由题意,分析变量间的等量关系,能建立当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(Ⅱ)①由已知条件利用100天玫瑰花的日需求量(单位:枝),整理得表格,能求出这100天的日利润(单位:元)的平均数.
②利润不少于75元,当且仅当日需求量不少于16枝,由此能求出当天的利润不少于75元的概率.
试题解析:
(1)当日需求量n≥17时,利润y=85.
当日需求量n<17时,利润y=10n-85.
所以y关于n的函数解析式为
y=![]() (n∈N).
(n∈N).
(2)①这100天中有10天的日利润为55元,20天的日利润为65元,16天的日利润为75元,54天的日利润为85元,所以这100天的日利润的平均数为![]() ×(55×10+65×20+75×16+85×54)=76.4.
×(55×10+65×20+75×16+85×54)=76.4.
②利润不低于75元当且仅当日需求量不少于16枝.故当天的利润不少于75元的概率为P=0.16+0.16+0.15+0.13+0.1=0.7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图所示的频率分布直方图.
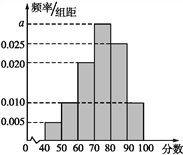
(1)求图中实数a的值;
(2)若该校高二年级共有学生640人,试估计该校高二年级期中考试数学成绩不低于60分的学生人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=m﹣|x﹣2|,m∈R,且f(x+2)≥0的解集为[﹣3,3].
(Ⅰ)解不等式:f(x)+f(x+2)>0;
(Ⅱ)若a,b,c均为正实数,且满足a+b+c=m,求证: +
+  +
+  ≥3.
≥3. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在(
 ﹣
﹣  )n的展开式中,第6项为常数项.
)n的展开式中,第6项为常数项.
(1)求n;
(2)求含x2项的系数;
(3)求展开式中所有的有理项. -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
-
科目: 来源: 题型:
查看答案和解析>>【题目】一批产品中,有一级品100个,二级品60个,三级品40个,分别用系统抽样和分层抽样的方法,从这批产品中抽取一个容量为20的样本,写出抽样过程,并说明采用哪种抽样方法更能反映总体水平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了对某课题进行讨论研究,用分层抽样的方法从三所高校A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
高校
相关人数
抽取人数
A
x
1
B
36
y
C
54
3
(1)求x、y;
(2)若从高校B相关的人中选2人作专题发言,应采用什么抽样法,请写出合理的抽样过程.
相关试题

