【题目】所谓正三棱锥,指的是底面为正三角形,顶点在底面上的射影为底面三角形中心的三棱锥,在正三棱锥S﹣ABC中,M是SC的中点,且AM⊥SB,底面边长AB=2 ![]() ,则正三棱锥S﹣ABC的体积为 , 其外接球的表面积为 .
,则正三棱锥S﹣ABC的体积为 , 其外接球的表面积为 .
参考答案:
【答案】![]() ;12π
;12π
【解析】解:设O为S在底面ABC的投影,则O为等边三角形ABC的中心,
∵SO⊥平面ABC,AC平面ABC,
∴AC⊥SO,又BO⊥AC,
∴AC⊥平面SBO,∵SB平面SBO,
∴SB⊥AC,又AM⊥SB,AM平面SAC,AC平面SAC,AM∩AC=A,
∴SB⊥平面SAC,
同理可证SC⊥平面SAB.
∴SA,SB,SC两两垂直.
∵△SOA≌△SOB≌△SOC,
∴SA=SB=SC,
∵AB=2 ![]() ,∴SA=SB=SC=2.
,∴SA=SB=SC=2.
∴三棱锥的体积V= ![]() =
= ![]() .
.
设外接球球心为N,则N在SO上.
∵BO= ![]() =
= ![]() .∴SO=
.∴SO= ![]() =
= ![]() ,
,
设外接球半径为r,则NO=SO﹣r= ![]() ﹣r,NB=r,
﹣r,NB=r,
∵OB2+ON2=NB2 , ∴ ![]() +(
+( ![]() )2=r2 , 解得r=
)2=r2 , 解得r= ![]() .
.
∴外接球的表面积S=4π×3=12π.
所以答案是: ![]() ,12π.
,12π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}满足:a3=4,a5+a7=14,{an}的前n项和为Sn .
(1)求an及Sn;
(2)令bn= (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某矿山企业生产某产品的年固定成本为
 万元,每生产千件该产品需另投入
万元,每生产千件该产品需另投入 万元,设该企业年内共生产此种产品
万元,设该企业年内共生产此种产品 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为 万元,且
万元,且
(Ⅰ)写出年利润
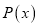 (万元)关于产品年产量
(万元)关于产品年产量 (千件)的函数关系式;
(千件)的函数关系式;(Ⅱ)问:年产量
 为多少千件时,该企业生产此产品所获年利润最大?
为多少千件时,该企业生产此产品所获年利润最大?注:年利润=年销售收入-年总成本.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
① “若
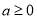 ,则
,则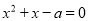 有实根”的逆否命题为真命题;
有实根”的逆否命题为真命题;②命题“
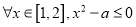 ”为真命题的一个充分不必要条件是
”为真命题的一个充分不必要条件是 ;
;③命题“
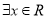 ,使得
,使得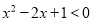 ”的否定是真命题;
”的否定是真命题;④命题
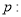 函数
函数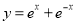 为偶函数,命题
为偶函数,命题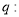 函数
函数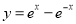 在
在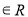 上为增函数,
上为增函数,则
 为真命题.
为真命题.其中,正确的命题是( )
A. ①② B. ①③ C. ②③ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
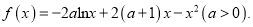
(Ⅰ)若函数
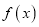 的图像在点
的图像在点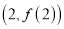 处的切线与直线
处的切线与直线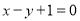 平行,求实数
平行,求实数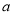 的值;
的值;(Ⅱ)讨论函数
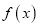 的单调性;
的单调性;(Ⅲ)若
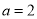 时,在
时,在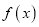 定义域内总有
定义域内总有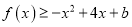 成立,试求实数
成立,试求实数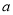 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某矿山企业生产某产品的年固定成本为
 万元,每生产千件该产品需另投入
万元,每生产千件该产品需另投入 万元,设该企业年内共生产此种产品
万元,设该企业年内共生产此种产品 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为 万元,且
万元,且
(Ⅰ)写出年利润
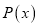 (万元)关于产品年产量
(万元)关于产品年产量 (千件)的函数关系式;
(千件)的函数关系式;(Ⅱ)问:年产量
 为多少千件时,该企业生产此产品所获年利润最大?
为多少千件时,该企业生产此产品所获年利润最大?注:年利润=年销售收入-年总成本.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个棱长为a的正方体嵌入到四个半径为1且两两相切的实心小球所形成的球间空隙内,使得正方体能够任意自由地转动,则a的最大值为 .
相关试题

