【题目】若函数 ![]() 的图象向左平移
的图象向左平移 ![]() 个单位,得到函数g(x)的图象,则下列关于g(x)叙述正确的是( )
个单位,得到函数g(x)的图象,则下列关于g(x)叙述正确的是( )
A.g(x)的最小正周期为2π
B.g(x)在 ![]() 内单调递增
内单调递增
C.g(x)的图象关于 ![]() 对称
对称
D.g(x)的图象关于 ![]() 对称
对称
参考答案:
【答案】C
【解析】解:函数 ![]() . 化简可得:f(x)=sin2x﹣
. 化简可得:f(x)=sin2x﹣ ![]() sinxcosx=
sinxcosx= ![]() -
- ![]() cos2x﹣
cos2x﹣ ![]() sin2x
sin2x
= ![]() ﹣sin(2x+
﹣sin(2x+ ![]() )图象向左平移
)图象向左平移 ![]() 个单位,可得:
个单位,可得: ![]() ﹣sin(2x+
﹣sin(2x+ ![]() +
+ ![]() )=
)= ![]() -sin(2x+
-sin(2x+ ![]() )=g(x)
)=g(x)
最小正周期T= ![]() ,∴A不对.
,∴A不对.
由 ![]() ≤2x+
≤2x+ ![]() ,可得:
,可得: ![]() ,g(x)在
,g(x)在 ![]() 内单调递增,∴B不对.
内单调递增,∴B不对.
由2x+ ![]() =
= ![]() ,可得x=
,可得x= ![]() ,(k∈Z),当k=0时,可得g(x)的图象的对称轴为
,(k∈Z),当k=0时,可得g(x)的图象的对称轴为 ![]() ,
,
∴C对.
由2x+ ![]() =kπ,可得x=
=kπ,可得x= ![]() ﹣
﹣ ![]() ,对称中心的横坐标为(
,对称中心的横坐标为( ![]() ,0),∴D不对.
,0),∴D不对.
故选C.
【考点精析】根据题目的已知条件,利用函数y=Asin(ωx+φ)的图象变换的相关知识可以得到问题的答案,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=
 AD,∠BAD=∠ABC=90°,E是PD的中点.
AD,∠BAD=∠ABC=90°,E是PD的中点.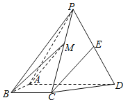
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C的圆心坐标
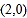 且与线y=3x+4相切,
且与线y=3x+4相切,(1)求圆C的方程;
(2)设直线
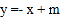 与圆C交于M,N两点,那么以MN为直径的圆能否经过原点,若能,请求出直线MN的方程;若不能,请说明理由.
与圆C交于M,N两点,那么以MN为直径的圆能否经过原点,若能,请求出直线MN的方程;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知定义在R上的函数f(x)=|x﹣m|+|x|,m∈N* , 存在实数x使f(x)<2成立.
(Ⅰ)求实数m的值;
(Ⅱ)若α,β>1,f(α)+f(β)=2,求证: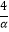 +
+ 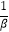 ≥
≥  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
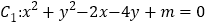
(1)若曲线C1是一个圆,且点P(1,1)在圆C1外,求实数m的取值范围;
(2)当m=2时,曲线
 关于直线x+1=0对称的曲线为
关于直线x+1=0对称的曲线为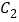 ,设P为平面上的点,满足:存在过P点的无穷多对互相垂直的直线
,设P为平面上的点,满足:存在过P点的无穷多对互相垂直的直线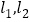 ,它们分别与曲线C1和曲线
,它们分别与曲线C1和曲线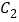 相交,且直线
相交,且直线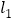 被曲线C1截得的弦长与直线l2被曲线C2截得的弦长总相等.求所有满足条件的点P的坐标;
被曲线C1截得的弦长与直线l2被曲线C2截得的弦长总相等.求所有满足条件的点P的坐标; -
科目: 来源: 题型:
查看答案和解析>>【题目】若命题p:从有2件正品和2件次品的产品中任选2件得到都是正品的概率为三分之一;命题q:在边长为4的正方形ABCD内任取一点M,则∠AMB>90°的概率为
 ,则下列命题是真命题的是( )
,则下列命题是真命题的是( )
A.p∧q
B.(p)∧q
C.p∧(q)
D.q -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将
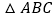 沿DE,EF,DF折成正四面体
沿DE,EF,DF折成正四面体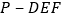 ,则在此正四面体中,下列说法正确的是______.
,则在此正四面体中,下列说法正确的是______.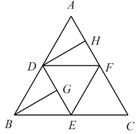
 异面直线PG与DH所成的角的余弦值为
异面直线PG与DH所成的角的余弦值为 ;
;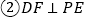 ;
;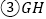 与PD所成的角为
与PD所成的角为 ;
;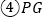 与EF所成角为
与EF所成角为
相关试题

