【题目】如图,在边长为4的正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将![]() 沿DE,EF,DF折成正四面体
沿DE,EF,DF折成正四面体![]() ,则在此正四面体中,下列说法正确的是______.
,则在此正四面体中,下列说法正确的是______.
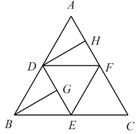
![]() 异面直线PG与DH所成的角的余弦值为
异面直线PG与DH所成的角的余弦值为![]() ;
;
![]() ;
;
![]() 与PD所成的角为
与PD所成的角为![]() ;
;
![]() 与EF所成角为
与EF所成角为![]()
参考答案:
【答案】![]()
【解析】
可证明![]() 平面
平面![]() ,可得
,可得![]() 正确;连接
正确;连接![]() ,取中点
,取中点![]() ,异面直线
,异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,由余弦定理可证明
,由余弦定理可证明![]() 正确;取
正确;取![]() 中点
中点![]() ,连接
,连接![]() ,异面
,异面![]() 与
与![]() 所成的角为
所成的角为![]() ,由余弦定理可得
,由余弦定理可得![]() 不对;异面
不对;异面![]() 与
与![]() 所成角的为
所成角的为![]() ,由余弦定理可得
,由余弦定理可得![]() 不对,从而可得结果.
不对,从而可得结果.
![]() 的边长为4,折成正四面体
的边长为4,折成正四面体![]() 后,如图
后,如图

![]() ,E,F分别为各边的中点,G,H分别为DE,AF的中点,
,E,F分别为各边的中点,G,H分别为DE,AF的中点,
![]() ,
,![]() ;
;
连接FG,取中点M,可得![]() ,
,
![]() 异面直线PG与DH所成的角的平角为
异面直线PG与DH所成的角的平角为![]() ;
;
![]() ,
,![]()
连接MD,可得![]() .
.
![]() ;
;
在![]() 中,
中,
余弦定理:![]() ;
;![]() 对;
对;![]() 对;
对;
取DF中点N,连接GN,NH,可得![]()
异面GH与PD所成的角的平面角为![]() ,
,
由余弦定理,GH与PD所成的角不是![]() ;
;![]() 不对;
不对;
异面PG与EF所成角的平面角为![]() ,
,
由余弦定理,可得PG与EF所成角不是![]() 不对.
不对.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
 的图象向左平移
的图象向左平移 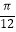 个单位,得到函数g(x)的图象,则下列关于g(x)叙述正确的是( )
个单位,得到函数g(x)的图象,则下列关于g(x)叙述正确的是( )
A.g(x)的最小正周期为2π
B.g(x)在 内单调递增
内单调递增
C.g(x)的图象关于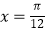 对称
对称
D.g(x)的图象关于 对称
对称 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
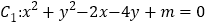
(1)若曲线C1是一个圆,且点P(1,1)在圆C1外,求实数m的取值范围;
(2)当m=2时,曲线
 关于直线x+1=0对称的曲线为
关于直线x+1=0对称的曲线为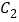 ,设P为平面上的点,满足:存在过P点的无穷多对互相垂直的直线
,设P为平面上的点,满足:存在过P点的无穷多对互相垂直的直线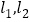 ,它们分别与曲线C1和曲线
,它们分别与曲线C1和曲线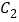 相交,且直线
相交,且直线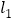 被曲线C1截得的弦长与直线l2被曲线C2截得的弦长总相等.求所有满足条件的点P的坐标;
被曲线C1截得的弦长与直线l2被曲线C2截得的弦长总相等.求所有满足条件的点P的坐标; -
科目: 来源: 题型:
查看答案和解析>>【题目】若命题p:从有2件正品和2件次品的产品中任选2件得到都是正品的概率为三分之一;命题q:在边长为4的正方形ABCD内任取一点M,则∠AMB>90°的概率为
 ,则下列命题是真命题的是( )
,则下列命题是真命题的是( )
A.p∧q
B.(p)∧q
C.p∧(q)
D.q -
科目: 来源: 题型:
查看答案和解析>>【题目】某校书法兴趣组有3名男同学A,B,C和3名女同学X,Y,Z,其年级情况如下表:
一年级
二年级
三年级
男同学
A
B
C
女同学
X
Y
Z
现从这6名同学中随机选出2人参加书法比赛
 每人被选到的可能性相同
每人被选到的可能性相同 .
. 用表中字母列举出所有可能的结果;
用表中字母列举出所有可能的结果; 设M为事件“选出的2人来自不同年级且性别相同”,求事件M发生的概率.
设M为事件“选出的2人来自不同年级且性别相同”,求事件M发生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月15日中的某一天到达该市,并停留2天.
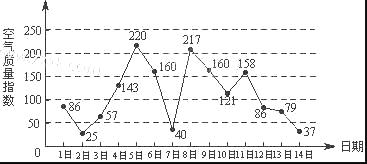
(Ⅰ)求此人到达当日空气质量优良的概率;
(Ⅱ)求此人在该市停留期间只有1天空气重度污染的概率;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数列{an}中,设f(n)=an , 且f(n)满足f(n+1)﹣2f(n)=2n(n∈N*),且a1=1.
(1)设 ,证明数列{bn}为等差数列;
,证明数列{bn}为等差数列;
(2)求数列{an}的前n项和Sn .
相关试题

